Step-8: Advanced topics¶
Since we now have explored the basic features of pySDC, we are actually ready to do some serious science (e.g. in the projects). However, we gather here further interesting cases, e.g. special flags or more alternative implementations of components.
Part A: Visualizing Residuals¶
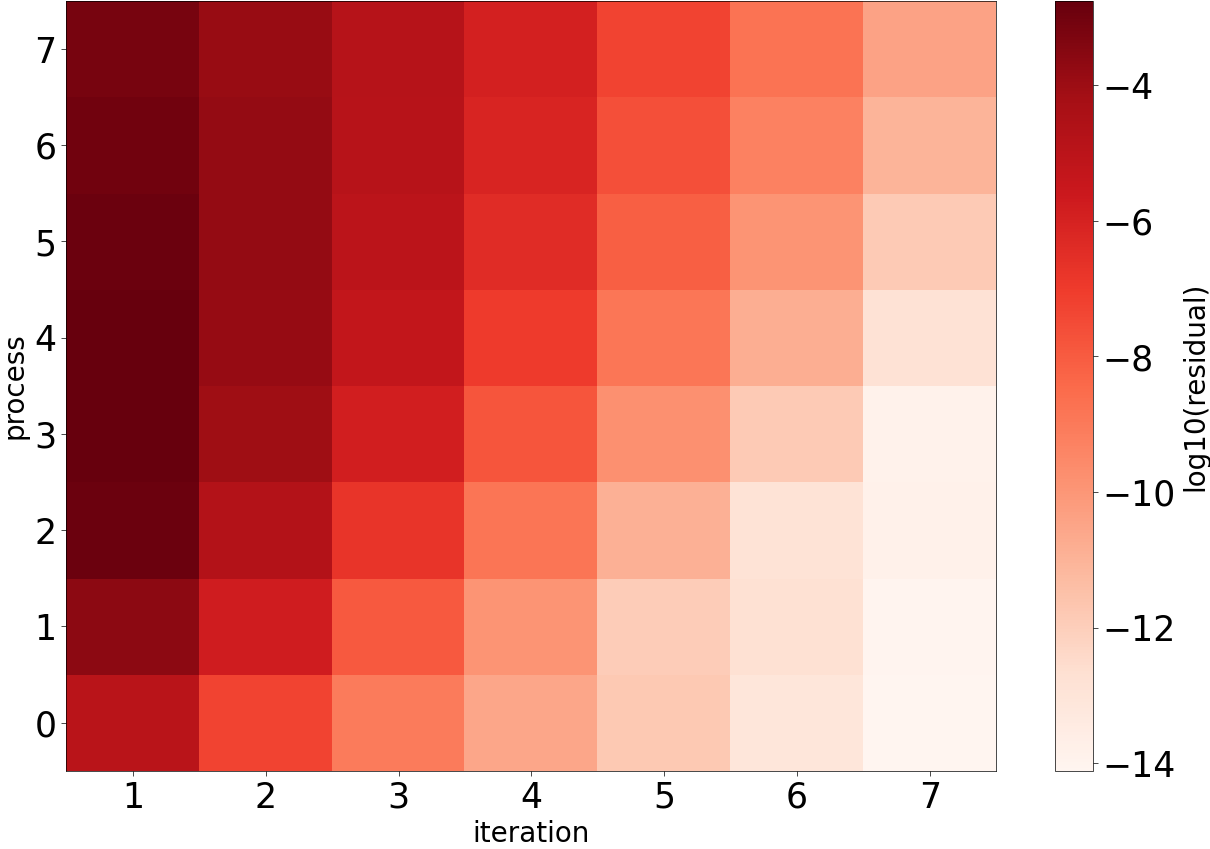
In this part, we briefly introduce the visualization of residuals, built in into pySDC’s plugins.
The application is (supposed) to be simple: merely put the stats object into the function show_residual_across_simulation and look at the resulting figure.
Important things to note:
The function visualizes simply the residuals over all processes and all iterations, but only for a single block.
The function itself is pretty straightforward and does not require passing the number of processes or iterations.
Full code: pySDC/tutorial/step_8/A_visualize_residuals.py
import os
from pathlib import Path
from pySDC.helpers.stats_helper import get_sorted
from pySDC.helpers.visualization_tools import show_residual_across_simulation
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.tutorial.step_6.A_run_non_MPI_controller import set_parameters_ml
def main():
"""
A simple test program to demonstrate residual visualization
"""
# get parameters from Step 6, Part A
description, controller_params, t0, Tend = set_parameters_ml()
# use 8 processes here
num_proc = 8
# instantiate controller
controller = controller_nonMPI(num_procs=num_proc, controller_params=controller_params, description=description)
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(t0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)
# compute exact solution and compare (for testing purposes only)
uex = P.u_exact(Tend)
err = abs(uex - uend)
# filter statistics by type (number of iterations)
iter_counts = get_sorted(stats, type='niter', sortby='time')
# compute and print statistics
min_iter = 99
max_iter = 0
Path("data").mkdir(parents=True, exist_ok=True)
f = open('data/step_8_A_out.txt', 'w')
for item in iter_counts:
out = 'Number of iterations for time %4.2f: %1i' % item
f.write(out + '\n')
print(out)
min_iter = min(min_iter, item[1])
max_iter = max(max_iter, item[1])
f.close()
# call helper routine to produce residual plot
fname = 'data/step_8_residuals.png'
show_residual_across_simulation(stats=stats, fname=fname)
assert err < 6.1555e-05, 'ERROR: error is too large, got %s' % err
assert os.path.isfile(fname), 'ERROR: residual plot has not been created'
assert min_iter == 7 and max_iter == 7, "ERROR: number of iterations not as expected, got %s and %s" % (
min_iter,
max_iter,
)
if __name__ == "__main__":
main()
Results:
Number of iterations for time 0.00: 7
Number of iterations for time 0.12: 7
Number of iterations for time 0.25: 7
Number of iterations for time 0.38: 7
Number of iterations for time 0.50: 7
Number of iterations for time 0.62: 7
Number of iterations for time 0.75: 7
Number of iterations for time 0.88: 7
Part B: Multi-step SDC¶
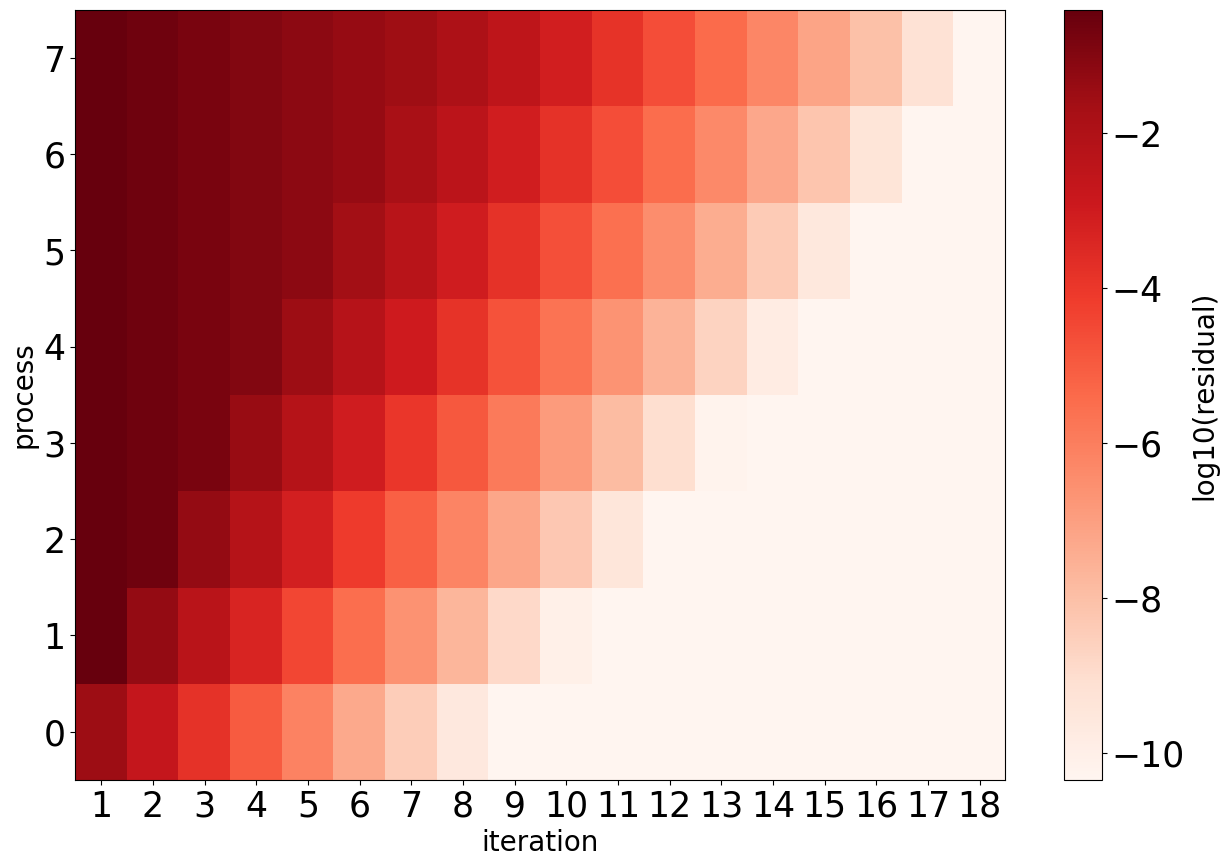
One interesting question when playing around with the different configurations is this: what happens, if we want parallel time-steps but only a single level? The result is called multi-step SDC. Here, after each sweep the result is sent forward, but is picked up in the next (and not current) iteration. This corresponds to performing only the smoother stage in a multigrid scheme. Parallelization is dead-simple and no coarsening strategy is needed. Yet, the missing stabilization of the coarse level leads to a significant increase in iterations, when more time-steps are computed in parallel. To prevent this, information can be sent forward immediately, but then this is not a parallel algorithm anymore..
Important things to note:
Use the controller parameter
mssdc_jacto control whether the method should be “parallel” (Jacobi-like) or “serial” (Gauss-like).We increased the logging value here again, (safely) ignoring the warnings for multi-step SDC.
Full code: pySDC/tutorial/step_8/B_multistep_SDC.py
import os
from pathlib import Path
from pySDC.helpers.stats_helper import get_sorted
from pySDC.helpers.visualization_tools import show_residual_across_simulation
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.HeatEquation_ND_FD import heatNd_unforced
from pySDC.implementations.sweeper_classes.generic_implicit import generic_implicit
from pySDC.implementations.transfer_classes.TransferMesh import mesh_to_mesh
def main():
"""
A simple test program to do compare PFASST with multi-step SDC
"""
# initialize level parameters
level_params = dict()
level_params['restol'] = 5e-10
level_params['dt'] = 0.125
# initialize sweeper parameters
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = [3]
sweeper_params['QI'] = 'LU'
# initialize problem parameters
problem_params = dict()
problem_params['nu'] = 0.1 # diffusion coefficient
problem_params['freq'] = 2 # frequency for the test value
problem_params['bc'] = 'dirichlet-zero' # boundary conditions
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 50
# initialize space transfer parameters
space_transfer_params = dict()
space_transfer_params['rorder'] = 2
space_transfer_params['iorder'] = 6
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 40
# fill description dictionary for easy step instantiation
description = dict()
description['problem_class'] = heatNd_unforced
description['sweeper_class'] = generic_implicit
description['sweeper_params'] = sweeper_params
description['level_params'] = level_params
description['step_params'] = step_params
description['space_transfer_class'] = mesh_to_mesh
description['space_transfer_params'] = space_transfer_params
# set up parameters for PFASST run
problem_params['nvars'] = [63, 31]
description['problem_params'] = problem_params.copy()
description_pfasst = description.copy()
# set up parameters for MSSDC run
problem_params['nvars'] = [63]
description['problem_params'] = problem_params.copy()
description_mssdc = description.copy()
controller_params['mssdc_jac'] = True
controller_params_jac = controller_params.copy()
controller_params['mssdc_jac'] = False
controller_params_gs = controller_params.copy()
# set time parameters
t0 = 0.0
Tend = 1.0
# set up list of parallel time-steps to run PFASST/MSSDC with
num_proc = 8
# instantiate controllers
controller_mssdc_jac = controller_nonMPI(
num_procs=num_proc, controller_params=controller_params_jac, description=description_mssdc
)
controller_mssdc_gs = controller_nonMPI(
num_procs=num_proc, controller_params=controller_params_gs, description=description_mssdc
)
controller_pfasst = controller_nonMPI(
num_procs=num_proc, controller_params=controller_params, description=description_pfasst
)
# get initial values on finest level
P = controller_mssdc_jac.MS[0].levels[0].prob
uinit = P.u_exact(t0)
# call main functions to get things done...
uend_pfasst, stats_pfasst = controller_pfasst.run(u0=uinit, t0=t0, Tend=Tend)
uend_mssdc_jac, stats_mssdc_jac = controller_mssdc_jac.run(u0=uinit, t0=t0, Tend=Tend)
uend_mssdc_gs, stats_mssdc_gs = controller_mssdc_gs.run(u0=uinit, t0=t0, Tend=Tend)
# compute exact solution and compare for both runs
uex = P.u_exact(Tend)
err_mssdc_jac = abs(uex - uend_mssdc_jac)
err_mssdc_gs = abs(uex - uend_mssdc_gs)
err_pfasst = abs(uex - uend_pfasst)
diff_jac = abs(uend_mssdc_jac - uend_pfasst)
diff_gs = abs(uend_mssdc_gs - uend_pfasst)
diff_jac_gs = abs(uend_mssdc_gs - uend_mssdc_jac)
Path("data").mkdir(parents=True, exist_ok=True)
f = open('data/step_8_B_out.txt', 'w')
out = 'Error PFASST: %12.8e' % err_pfasst
f.write(out + '\n')
print(out)
out = 'Error parallel MSSDC: %12.8e' % err_mssdc_jac
f.write(out + '\n')
print(out)
out = 'Error serial MSSDC: %12.8e' % err_mssdc_gs
f.write(out + '\n')
print(out)
out = 'Diff PFASST vs. parallel MSSDC: %12.8e' % diff_jac
f.write(out + '\n')
print(out)
out = 'Diff PFASST vs. serial MSSDC: %12.8e' % diff_gs
f.write(out + '\n')
print(out)
out = 'Diff parallel vs. serial MSSDC: %12.8e' % diff_jac_gs
f.write(out + '\n')
print(out)
# convert filtered statistics to list of iterations count, sorted by process
iter_counts_pfasst = get_sorted(stats_pfasst, type='niter', sortby='time')
iter_counts_mssdc_jac = get_sorted(stats_mssdc_jac, type='niter', sortby='time')
iter_counts_mssdc_gs = get_sorted(stats_mssdc_gs, type='niter', sortby='time')
# compute and print statistics
for item_pfasst, item_mssdc_jac, item_mssdc_gs in zip(
iter_counts_pfasst, iter_counts_mssdc_jac, iter_counts_mssdc_gs
):
out = 'Number of iterations for time %4.2f (PFASST/parMSSDC/serMSSDC): %2i / %2i / %2i' % (
item_pfasst[0],
item_pfasst[1],
item_mssdc_jac[1],
item_mssdc_gs[1],
)
f.write(out + '\n')
print(out)
f.close()
# call helper routine to produce residual plot
show_residual_across_simulation(stats_mssdc_jac, 'data/step_8_residuals_mssdc_jac.png')
show_residual_across_simulation(stats_mssdc_gs, 'data/step_8_residuals_mssdc_gs.png')
assert os.path.isfile('data/step_8_residuals_mssdc_jac.png')
assert os.path.isfile('data/step_8_residuals_mssdc_gs.png')
assert diff_jac < 3.1e-10, (
"ERROR: difference between PFASST and parallel MSSDC controller is too large, got %s" % diff_jac
)
assert diff_gs < 3.1e-10, (
"ERROR: difference between PFASST and serial MSSDC controller is too large, got %s" % diff_gs
)
assert diff_jac_gs < 3.1e-10, (
"ERROR: difference between parallel and serial MSSDC controller is too large, got %s" % diff_jac_gs
)
if __name__ == "__main__":
main()
Results:
Error PFASST: 2.87344391e-07
Error parallel MSSDC: 2.87650037e-07
Error serial MSSDC: 2.87540078e-07
Diff PFASST vs. parallel MSSDC: 3.05646470e-10
Diff PFASST vs. serial MSSDC: 1.95687262e-10
Diff parallel vs. serial MSSDC: 1.09959215e-10
Number of iterations for time 0.00 (PFASST/parMSSDC/serMSSDC): 5 / 8 / 8
Number of iterations for time 0.12 (PFASST/parMSSDC/serMSSDC): 5 / 10 / 9
Number of iterations for time 0.25 (PFASST/parMSSDC/serMSSDC): 6 / 11 / 9
Number of iterations for time 0.38 (PFASST/parMSSDC/serMSSDC): 6 / 13 / 10
Number of iterations for time 0.50 (PFASST/parMSSDC/serMSSDC): 7 / 14 / 10
Number of iterations for time 0.62 (PFASST/parMSSDC/serMSSDC): 7 / 15 / 11
Number of iterations for time 0.75 (PFASST/parMSSDC/serMSSDC): 8 / 16 / 11
Number of iterations for time 0.88 (PFASST/parMSSDC/serMSSDC): 8 / 18 / 11
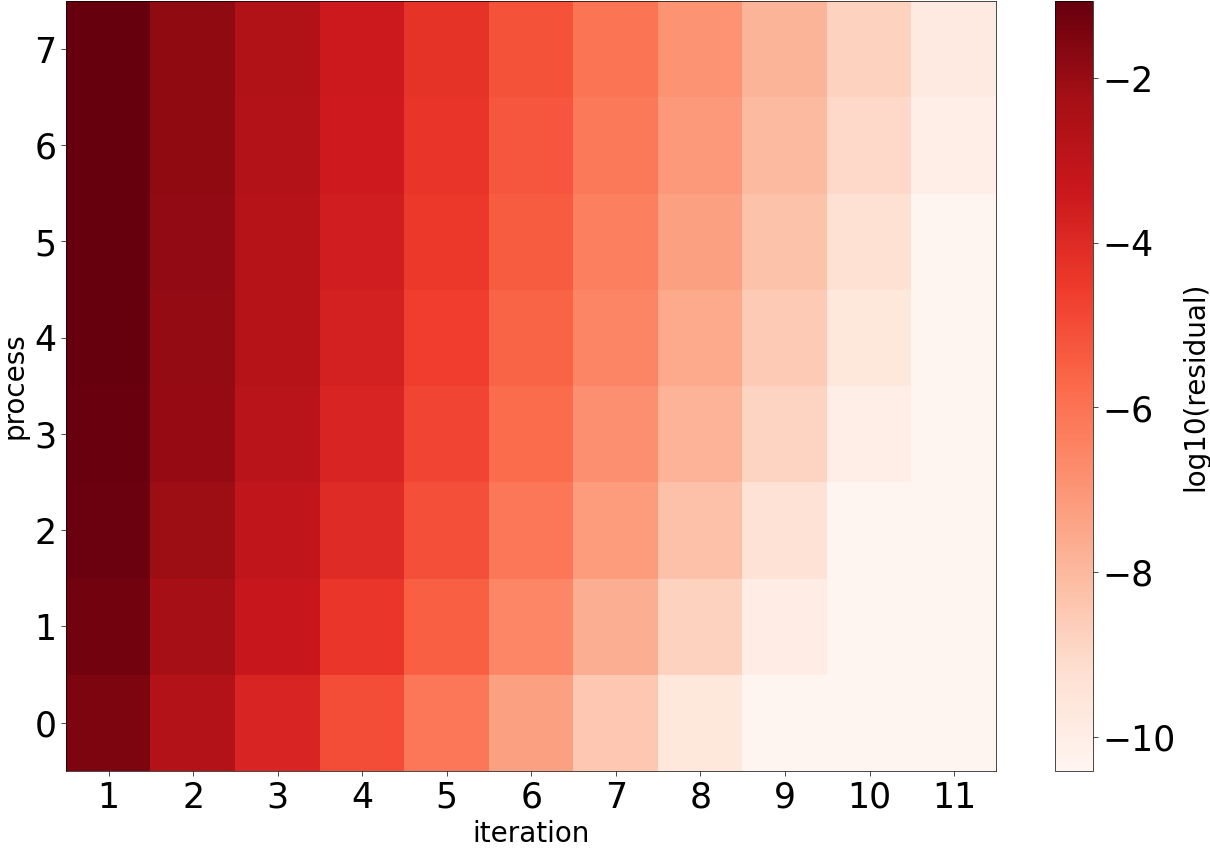
Part C: Iteration estimator¶
One may ask when to stop the SDC, MLSDC, PFASST iterations. So far, we have used a residual threshold or a fixed number of iterations to stop the process. Another option is to estimate the number of iterations it takes to reach a given error w.r.t. the exact collocation solution. This can be done by using two consecutive iterates to estimate the Lipschitz constant of the iteration procedure. Adding a few magic/safety constants here and there and you can guess when to stop. This example takes three different test cases and checks how well the iteration estimator drives the iterates below the threshold.
Important things to note:
The estimator also works for PFASST, where is ensures that up to each step (!) the tolerance is met.
The method also works for the parallel controller_MPI controller by using interrupts for checking when to stop (not tested here).
Full code: pySDC/tutorial/step_8/C_iteration_estimator.py
import numpy as np
from pathlib import Path
from pySDC.helpers.stats_helper import get_sorted
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.HeatEquation_ND_FD import heatNd_forced
from pySDC.implementations.problem_classes.AdvectionEquation_ND_FD import advectionNd
from pySDC.implementations.problem_classes.Auzinger_implicit import auzinger
from pySDC.implementations.sweeper_classes.imex_1st_order import imex_1st_order
from pySDC.implementations.sweeper_classes.generic_implicit import generic_implicit
from pySDC.implementations.transfer_classes.TransferMesh import mesh_to_mesh
from pySDC.implementations.transfer_classes.TransferMesh_NoCoarse import mesh_to_mesh as mesh_to_mesh_nc
from pySDC.implementations.convergence_controller_classes.check_iteration_estimator import CheckIterationEstimatorNonMPI
from pySDC.tutorial.step_8.HookClass_error_output import error_output
def setup_diffusion(dt=None, ndim=None, ml=False):
# initialize level parameters
level_params = dict()
level_params['restol'] = 1e-10
level_params['dt'] = dt # time-step size
level_params['nsweeps'] = 1
# initialize sweeper parameters
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = 3
sweeper_params['QI'] = ['LU'] # For the IMEX sweeper, the LU-trick can be activated for the implicit part
# sweeper_params['initial_guess'] = 'zero'
# initialize problem parameters
problem_params = dict()
problem_params['order'] = 8 # order of accuracy for FD discretization in space
problem_params['nu'] = 0.1 # diffusion coefficient
problem_params['bc'] = 'periodic' # boundary conditions
problem_params['freq'] = tuple(2 for _ in range(ndim)) # frequencies
if ml:
problem_params['nvars'] = [tuple(64 for _ in range(ndim)), tuple(32 for _ in range(ndim))] # number of dofs
else:
problem_params['nvars'] = tuple(64 for _ in range(ndim)) # number of dofs
problem_params['solver_type'] = 'CG' # do CG instead of LU
problem_params['liniter'] = 10 # number of CG iterations
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 50
step_params['errtol'] = 1e-07
# initialize space transfer parameters
space_transfer_params = dict()
space_transfer_params['rorder'] = 2
space_transfer_params['iorder'] = 6
space_transfer_params['periodic'] = True
# setup the iteration estimator
convergence_controllers = dict()
convergence_controllers[CheckIterationEstimatorNonMPI] = {'errtol': 1e-7}
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
controller_params['hook_class'] = error_output
# fill description dictionary for easy step instantiation
description = dict()
description['problem_class'] = heatNd_forced # pass problem class
description['problem_params'] = problem_params # pass problem parameters
description['sweeper_class'] = imex_1st_order # pass sweeper (see part B)
description['sweeper_params'] = sweeper_params # pass sweeper parameters
description['level_params'] = level_params # pass level parameters
description['step_params'] = step_params # pass step parameters
description['convergence_controllers'] = convergence_controllers
if ml:
description['space_transfer_class'] = mesh_to_mesh # pass spatial transfer class
description['space_transfer_params'] = space_transfer_params # pass parameters for spatial transfer
return description, controller_params
def setup_advection(dt=None, ndim=None, ml=False):
# initialize level parameters
level_params = dict()
level_params['restol'] = 1e-10
level_params['dt'] = dt # time-step size
level_params['nsweeps'] = 1
# initialize sweeper parameters
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = 3
sweeper_params['QI'] = ['LU'] # For the IMEX sweeper, the LU-trick can be activated for the implicit part
# sweeper_params['initial_guess'] = 'zero'
# initialize problem parameters
problem_params = dict()
problem_params['order'] = 6 # order of accuracy for FD discretization in space
problem_params['stencil_type'] = 'center' # order of accuracy for FD discretization in space
problem_params['bc'] = 'periodic' # boundary conditions
problem_params['c'] = 0.1 # diffusion coefficient
problem_params['freq'] = tuple(2 for _ in range(ndim)) # frequencies
if ml:
problem_params['nvars'] = [tuple(64 for _ in range(ndim)), tuple(32 for _ in range(ndim))] # number of dofs
else:
problem_params['nvars'] = tuple(64 for _ in range(ndim)) # number of dofs
problem_params['solver_type'] = 'GMRES' # do GMRES instead of LU
problem_params['liniter'] = 10 # number of GMRES iterations
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 50
step_params['errtol'] = 1e-07
# initialize space transfer parameters
space_transfer_params = dict()
space_transfer_params['rorder'] = 2
space_transfer_params['iorder'] = 6
space_transfer_params['periodic'] = True
# setup the iteration estimator
convergence_controllers = dict()
convergence_controllers[CheckIterationEstimatorNonMPI] = {'errtol': 1e-7}
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
controller_params['hook_class'] = error_output
# fill description dictionary for easy step instantiation
description = dict()
description['problem_class'] = advectionNd
description['problem_params'] = problem_params # pass problem parameters
description['sweeper_class'] = generic_implicit
description['sweeper_params'] = sweeper_params # pass sweeper parameters
description['level_params'] = level_params # pass level parameters
description['step_params'] = step_params # pass step parameters
description['convergence_controllers'] = convergence_controllers
if ml:
description['space_transfer_class'] = mesh_to_mesh # pass spatial transfer class
description['space_transfer_params'] = space_transfer_params # pass parameters for spatial transfer
return description, controller_params
def setup_auzinger(dt=None, ml=False):
# initialize level parameters
level_params = dict()
level_params['restol'] = 1e-10
level_params['dt'] = dt # time-step size
level_params['nsweeps'] = 1
# initialize sweeper parameters
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
if ml:
sweeper_params['num_nodes'] = [3, 2]
else:
sweeper_params['num_nodes'] = 3
sweeper_params['QI'] = ['LU'] # For the IMEX sweeper, the LU-trick can be activated for the implicit part
# sweeper_params['initial_guess'] = 'zero'
# initialize problem parameters
problem_params = dict()
problem_params['newton_tol'] = 1e-12
problem_params['newton_maxiter'] = 10
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 50
step_params['errtol'] = 1e-07
# setup the iteration estimator
convergence_controllers = dict()
convergence_controllers[CheckIterationEstimatorNonMPI] = {'errtol': 1e-7}
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
controller_params['hook_class'] = error_output
# fill description dictionary for easy step instantiation
description = dict()
description['problem_class'] = auzinger
description['problem_params'] = problem_params # pass problem parameters
description['sweeper_class'] = generic_implicit
description['sweeper_params'] = sweeper_params # pass sweeper parameters
description['level_params'] = level_params # pass level parameters
description['step_params'] = step_params # pass step parameters
description['convergence_controllers'] = convergence_controllers
if ml:
description['space_transfer_class'] = mesh_to_mesh_nc # pass spatial transfer class
return description, controller_params
def run_simulations(type=None, ndim_list=None, Tend=None, nsteps_list=None, ml=False, nprocs=None):
"""
A simple test program to do SDC runs for the heat equation in various dimensions
"""
t0 = None
dt = None
description = None
controller_params = None
Path("data").mkdir(parents=True, exist_ok=True)
f = open('data/step_8_C_out.txt', 'a')
for ndim in ndim_list:
for nsteps in nsteps_list:
if type == 'diffusion':
# set time parameters
t0 = 0.0
dt = (Tend - t0) / nsteps
description, controller_params = setup_diffusion(dt, ndim, ml)
mean_number_of_iterations = 3.00 if ml else 5.75
elif type == 'advection':
# set time parameters
t0 = 0.0
dt = (Tend - t0) / nsteps
description, controller_params = setup_advection(dt, ndim, ml)
mean_number_of_iterations = 2.00 if ml else 4.00
elif type == 'auzinger':
assert ndim == 1
# set time parameters
t0 = 0.0
dt = (Tend - t0) / nsteps
description, controller_params = setup_auzinger(dt, ml)
mean_number_of_iterations = 3.62 if ml else 5.62
out = f'Running {type} in {ndim} dimensions with time-step size {dt}...\n'
f.write(out + '\n')
print(out)
# Warning: this is black magic used to run an 'exact' collocation solver for each step within the hooks
description['step_params']['description'] = description
description['step_params']['controller_params'] = controller_params
# instantiate controller
controller = controller_nonMPI(
num_procs=nprocs, controller_params=controller_params, description=description
)
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(t0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)
# filter statistics by type (number of iterations)
iter_counts = get_sorted(stats, type='niter', sortby='time')
niters = np.array([item[1] for item in iter_counts])
out = f' Mean number of iterations: {np.mean(niters):4.2f}'
f.write(out + '\n')
print(out)
# filter statistics by type (error after time-step)
PDE_errors = get_sorted(stats, type='PDE_error_after_step', sortby='time')
coll_errors = get_sorted(stats, type='coll_error_after_step', sortby='time')
for iters, PDE_err, coll_err in zip(iter_counts, PDE_errors, coll_errors):
assert coll_err[1] < description['step_params']['errtol'], f'Error too high, got {coll_err[1]:8.4e}'
out = (
f' Errors after step {PDE_err[0]:8.4f} with {iters[1]} iterations: '
f'{PDE_err[1]:8.4e} / {coll_err[1]:8.4e}'
)
f.write(out + '\n')
print(out)
f.write('\n')
print()
# filter statistics by type (error after time-step)
timing = get_sorted(stats, type='timing_run', sortby='time')
out = f'...done, took {timing[0][1]} seconds!'
f.write(out + '\n')
print(out)
print()
out = '-----------------------------------------------------------------------------'
f.write(out + '\n')
print(out)
f.close()
assert np.isclose(
mean_number_of_iterations, np.mean(niters), atol=1e-2
), f'Expected \
{mean_number_of_iterations:.2f} mean iterations, but got {np.mean(niters):.2f}'
def main():
run_simulations(type='diffusion', ndim_list=[1], Tend=1.0, nsteps_list=[8], ml=False, nprocs=1)
run_simulations(type='diffusion', ndim_list=[1], Tend=1.0, nsteps_list=[8], ml=True, nprocs=1)
run_simulations(type='advection', ndim_list=[1], Tend=1.0, nsteps_list=[8], ml=False, nprocs=1)
run_simulations(type='advection', ndim_list=[1], Tend=1.0, nsteps_list=[8], ml=True, nprocs=1)
run_simulations(type='auzinger', ndim_list=[1], Tend=1.0, nsteps_list=[8], ml=False, nprocs=1)
run_simulations(type='auzinger', ndim_list=[1], Tend=1.0, nsteps_list=[8], ml=True, nprocs=1)
if __name__ == "__main__":
main()
Results:
Running diffusion in 1 dimensions with time-step size 0.125...
Mean number of iterations: 5.75
Errors after step 0.1250 with 5 iterations: 1.7804e-08 / 2.8422e-13
Errors after step 0.2500 with 5 iterations: 4.9619e-08 / 3.3040e-13
Errors after step 0.3750 with 6 iterations: 4.2300e-08 / 3.8769e-13
Errors after step 0.5000 with 6 iterations: 3.8684e-08 / 2.3270e-13
Errors after step 0.6250 with 6 iterations: 3.7128e-08 / 2.0370e-13
Errors after step 0.7500 with 6 iterations: 3.6619e-08 / 3.0886e-13
Errors after step 0.8750 with 6 iterations: 3.6530e-08 / 2.6684e-13
Errors after step 1.0000 with 6 iterations: 3.6478e-08 / 1.6026e-13
...done, took 0.34192614799997045 seconds!
-----------------------------------------------------------------------------
Running diffusion in 1 dimensions with time-step size 0.125...
Mean number of iterations: 3.00
Errors after step 0.1250 with 3 iterations: 9.8191e-09 / 3.1297e-13
Errors after step 0.2500 with 3 iterations: 1.7174e-08 / 2.5835e-13
Errors after step 0.3750 with 3 iterations: 2.2849e-08 / 2.2726e-13
Errors after step 0.5000 with 3 iterations: 2.7307e-08 / 2.7811e-13
Errors after step 0.6250 with 3 iterations: 3.0813e-08 / 2.8777e-13
Errors after step 0.7500 with 3 iterations: 3.3517e-08 / 1.9876e-13
Errors after step 0.8750 with 3 iterations: 3.5502e-08 / 3.3862e-13
Errors after step 1.0000 with 3 iterations: 3.6813e-08 / 2.4698e-13
...done, took 0.7710299400000054 seconds!
-----------------------------------------------------------------------------
Running advection in 1 dimensions with time-step size 0.125...
Mean number of iterations: 4.00
Errors after step 0.1250 with 4 iterations: 3.6459e-09 / 4.4409e-16
Errors after step 0.2500 with 4 iterations: 7.2907e-09 / 5.5511e-16
Errors after step 0.3750 with 4 iterations: 1.0930e-08 / 3.3307e-16
Errors after step 0.5000 with 4 iterations: 1.4571e-08 / 4.4409e-16
Errors after step 0.6250 with 4 iterations: 1.8225e-08 / 4.4409e-16
Errors after step 0.7500 with 4 iterations: 2.1875e-08 / 4.4409e-16
Errors after step 0.8750 with 4 iterations: 2.5517e-08 / 5.5511e-16
Errors after step 1.0000 with 4 iterations: 2.9147e-08 / 4.4409e-16
...done, took 0.20697575700000925 seconds!
-----------------------------------------------------------------------------
Running advection in 1 dimensions with time-step size 0.125...
Mean number of iterations: 2.00
Errors after step 0.1250 with 2 iterations: 3.7050e-09 / 3.1852e-13
Errors after step 0.2500 with 2 iterations: 7.4360e-09 / 3.1886e-13
Errors after step 0.3750 with 2 iterations: 1.1141e-08 / 3.1875e-13
Errors after step 0.5000 with 2 iterations: 1.4836e-08 / 3.1852e-13
Errors after step 0.6250 with 2 iterations: 1.8580e-08 / 3.1863e-13
Errors after step 0.7500 with 2 iterations: 2.2256e-08 / 3.1819e-13
Errors after step 0.8750 with 2 iterations: 2.5987e-08 / 3.1875e-13
Errors after step 1.0000 with 2 iterations: 2.9666e-08 / 3.1808e-13
...done, took 0.6084953490000089 seconds!
-----------------------------------------------------------------------------
Running auzinger in 1 dimensions with time-step size 0.125...
Mean number of iterations: 5.62
Errors after step 0.1250 with 5 iterations: 4.6598e-09 / 0.0000e+00
Errors after step 0.2500 with 5 iterations: 8.0010e-09 / 0.0000e+00
Errors after step 0.3750 with 5 iterations: 1.4700e-08 / 0.0000e+00
Errors after step 0.5000 with 6 iterations: 1.5583e-08 / 0.0000e+00
Errors after step 0.6250 with 6 iterations: 2.1829e-08 / 0.0000e+00
Errors after step 0.7500 with 6 iterations: 2.6153e-08 / 0.0000e+00
Errors after step 0.8750 with 6 iterations: 2.8266e-08 / 0.0000e+00
Errors after step 1.0000 with 6 iterations: 2.8338e-08 / 0.0000e+00
...done, took 0.13936675899998363 seconds!
-----------------------------------------------------------------------------
Running auzinger in 1 dimensions with time-step size 0.125...
Mean number of iterations: 3.62
Errors after step 0.1250 with 3 iterations: 4.2389e-09 / 0.0000e+00
Errors after step 0.2500 with 3 iterations: 8.4469e-09 / 0.0000e+00
Errors after step 0.3750 with 3 iterations: 1.1763e-08 / 0.0000e+00
Errors after step 0.5000 with 4 iterations: 1.7832e-08 / 0.0000e+00
Errors after step 0.6250 with 4 iterations: 2.3399e-08 / 0.0000e+00
Errors after step 0.7500 with 4 iterations: 2.8017e-08 / 0.0000e+00
Errors after step 0.8750 with 4 iterations: 3.1486e-08 / 0.0000e+00
Errors after step 1.0000 with 4 iterations: 3.3802e-08 / 0.0000e+00
...done, took 0.16292713600000752 seconds!
-----------------------------------------------------------------------------
Part X: To be continued…¶
We shall see what comes next…