Attempts to parallelize SDC¶
In this project, we test different strategies to parallelize SDC beyond PFASST. More precisely, the goal is to find a robust parallelization strategy within each iteration, i.e. parallelization across the collocation nodes. This code is used for the publication “Parallelizing SDC across the method”.
Different preconditioners for SDC¶
The easiest approach for a parallel SDC run is to parallelize the preconditioner, i.e. to find a diagonal Q-delta matrix. So far, this matrix is a lower triangular matrix, containing e.g. the Euler scheme or parts of the LU-decomposition of Q. Here, we study different ideas to work with a diagonal matrix and compare them to the standard schemes:
IEandLU: the standard scheme using implicit Euler or the LU trickIEpar: one Euler step from t0 to the current nodeQpar: Jacobi-like diagonal part of QMIN: A simple minimzation-based preconditioner
This part also contains minimization.py, producing the heat maps for the spectral radius of the stiff limit matrix.
Full code: pySDC/projects/parallelSDC/preconditioner_playground.py
import os
import pickle
from collections import namedtuple
import numpy as np
import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.AdvectionEquation_ND_FD import advectionNd
from pySDC.implementations.problem_classes.GeneralizedFisher_1D_FD_implicit import generalized_fisher
from pySDC.implementations.problem_classes.HeatEquation_ND_FD import heatNd_unforced
from pySDC.implementations.problem_classes.Van_der_Pol_implicit import vanderpol
from pySDC.implementations.sweeper_classes.generic_implicit import generic_implicit
ID = namedtuple('ID', ['setup', 'qd_type', 'param'])
def main():
# initialize level parameters (part I)
level_params = dict()
level_params['restol'] = 1e-08
# initialize sweeper parameters (part I)
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = 3
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 100
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
# set up list of Q-delta types and setups
qd_list = ['LU', 'IE', 'IEpar', 'Qpar', 'MIN', 'MIN3', 'MIN_GT']
setup_list = [
('heat', 63, [10.0**i for i in range(-3, 3)]),
('advection', 64, [10.0**i for i in range(-3, 3)]),
('vanderpol', 2, [0.1 * 2**i for i in range(0, 10)]),
('fisher', 63, [2**i for i in range(-2, 3)]),
]
# setup_list = [('fisher', 63, [2 * i for i in range(1, 6)])]
# pre-fill results with lists of setups
results = dict()
for setup, nvars, param_list in setup_list:
results[setup] = (nvars, param_list)
# loop over all Q-delta matrix types
for qd_type in qd_list:
# assign implicit Q-delta matrix
sweeper_params['QI'] = qd_type
# loop over all setups
for setup, nvars, param_list in setup_list:
# initialize problem parameters (part I)
problem_params = dict()
if setup != 'vanderpol':
problem_params['nvars'] = nvars # number of degrees of freedom for each level
# loop over all parameters
for param in param_list:
# fill description for the controller
description = dict()
description['sweeper_class'] = generic_implicit # pass sweeper
description['sweeper_params'] = sweeper_params # pass sweeper parameters
description['step_params'] = step_params # pass step parameters
print('working on: %s - %s - %s' % (qd_type, setup, param))
# decide which setup to take
if setup == 'heat':
problem_params['nu'] = param
problem_params['freq'] = 2
problem_params['bc'] = 'dirichlet-zero' # boundary conditions
level_params['dt'] = 0.1
description['problem_class'] = heatNd_unforced
description['problem_params'] = problem_params
description['level_params'] = level_params # pass level parameters
elif setup == 'advection':
problem_params['c'] = param
problem_params['order'] = 2
problem_params['freq'] = 2
problem_params['stencil_type'] = 'center' # boundary conditions
problem_params['bc'] = 'periodic' # boundary conditions
level_params['dt'] = 0.1
description['problem_class'] = advectionNd
description['problem_params'] = problem_params
description['level_params'] = level_params # pass level parameters
elif setup == 'vanderpol':
problem_params['newton_tol'] = 1e-09
problem_params['newton_maxiter'] = 20
problem_params['mu'] = param
problem_params['u0'] = np.array([2.0, 0])
level_params['dt'] = 0.1
description['problem_class'] = vanderpol
description['problem_params'] = problem_params
description['level_params'] = level_params
elif setup == 'fisher':
problem_params['nu'] = 1
problem_params['lambda0'] = param
problem_params['newton_maxiter'] = 20
problem_params['newton_tol'] = 1e-10
problem_params['interval'] = (-5, 5)
level_params['dt'] = 0.01
description['problem_class'] = generalized_fisher
description['problem_params'] = problem_params
description['level_params'] = level_params
else:
print('Setup not implemented..', setup)
exit()
# instantiate controller
controller = controller_nonMPI(
num_procs=1, controller_params=controller_params, description=description
)
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=0, Tend=level_params['dt'])
# filter statistics by type (number of iterations)
iter_counts = get_sorted(stats, type='niter', sortby='time')
# just one time-step, grep number of iteration and store
niter = iter_counts[0][1]
id = ID(setup=setup, qd_type=qd_type, param=param)
results[id] = niter
assert len(results) == (6 + 6 + 10 + 5) * 7 + 4, 'ERROR: did not get all results, got %s' % len(results)
# write out for later visualization
file = open('data/parallelSDC_iterations_precond.pkl', 'wb')
pickle.dump(results, file)
assert os.path.isfile('data/parallelSDC_iterations_precond.pkl'), 'ERROR: pickle did not create file'
def plot_iterations():
"""
Helper routine to plot iteration counts
"""
file = open('data/parallelSDC_iterations_precond.pkl', 'rb')
results = pickle.load(file)
# find the lists/header required for plotting
qd_type_list = []
setup_list = []
for key in results.keys():
if isinstance(key, ID):
if key.qd_type not in qd_type_list:
qd_type_list.append(key.qd_type)
elif isinstance(key, str):
setup_list.append(key)
print('Found these type of preconditioners:', qd_type_list)
print('Found these setups:', setup_list)
assert len(qd_type_list) == 7, 'ERROR did not find five preconditioners, got %s' % qd_type_list
assert len(setup_list) == 4, 'ERROR: did not find three setup, got %s' % setup_list
qd_type_list = ['LU', 'IE', 'IEpar', 'Qpar', 'MIN', 'MIN3', 'MIN_GT']
marker_list = [None, None, 's', 'o', '^', 'd', 'x']
color_list = ['k', 'k', 'r', 'g', 'b', 'c', 'm']
plt_helper.setup_mpl()
# loop over setups and Q-delta types: one figure per setup, all Qds in one plot
for setup in setup_list:
plt_helper.newfig(textwidth=238.96, scale=0.89)
for qd_type, marker, color in zip(qd_type_list, marker_list, color_list):
niter = np.zeros(len(results[setup][1]))
for key in results.keys():
if isinstance(key, ID):
if key.setup == setup and key.qd_type == qd_type:
xvalue = results[setup][1].index(key.param)
niter[xvalue] = results[key]
if qd_type == 'LU':
ls = '--'
lw = 0.5
elif qd_type == 'IE':
ls = '-.'
lw = 0.5
else:
ls = '-'
lw = 1
plt_helper.plt.semilogx(
results[setup][1],
niter,
label=qd_type,
lw=lw,
linestyle=ls,
color=color,
marker=marker,
markeredgecolor='k',
)
if setup == 'heat':
xlabel = r'$\nu$'
elif setup == 'advection':
xlabel = r'$c$'
elif setup == 'fisher':
xlabel = r'$\lambda_0$'
elif setup == 'vanderpol':
xlabel = r'$\mu$'
else:
print('Setup not implemented..', setup)
exit()
plt_helper.plt.ylim([0, 60])
plt_helper.plt.legend(loc=2, ncol=1)
plt_helper.plt.ylabel('number of iterations')
plt_helper.plt.xlabel(xlabel)
plt_helper.plt.grid()
# save plot as PDF and PGF
fname = 'data/parallelSDC_preconditioner_' + setup
plt_helper.savefig(fname)
assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
# assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'
if __name__ == "__main__":
main()
plot_iterations()
Results:
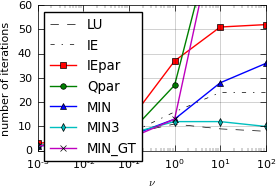
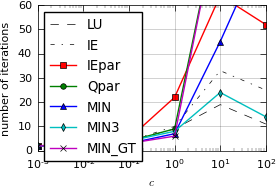
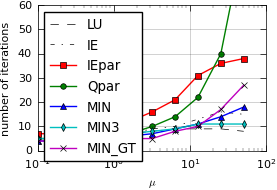
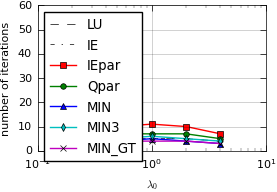
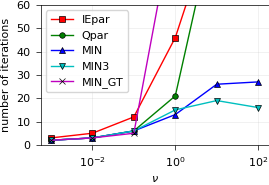
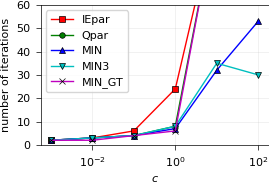
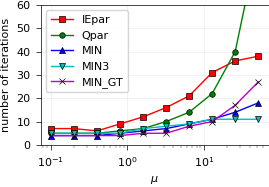
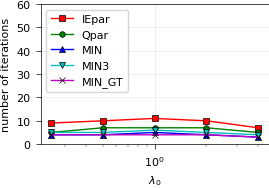
Node-parallel SDC with MPI¶
The project also contains a sweeper (and a transfer class) to allow real, MPI-based parallelism of diagonal preconditioners.
We test again the aforementioned ideas, but now add the MIN3 approach: These values have been obtained using Indie Solver,
a commercial solver for black-box optimization which aggregates several state-of-the-art optimization methods (free academic subscription plan).
The objective function in this case is the sum over 17^2 values of lamdt, real and imaginary. This works surprisingly well!
Full code: pySDC/projects/parallelSDC/preconditioner_playground_MPI.py
import os
import pickle
from collections import namedtuple
import numpy as np
from mpi4py import MPI
import argparse
import matplotlib as mpl
mpl.use("Agg")
import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.AdvectionEquation_ND_FD import advectionNd
from pySDC.implementations.problem_classes.GeneralizedFisher_1D_FD_implicit import generalized_fisher
from pySDC.implementations.problem_classes.HeatEquation_ND_FD import heatNd_unforced
from pySDC.implementations.problem_classes.Van_der_Pol_implicit import vanderpol
from pySDC.implementations.sweeper_classes.generic_implicit_MPI import generic_implicit_MPI
ID = namedtuple('ID', ['setup', 'qd_type', 'param'])
def main(comm=None):
# initialize level parameters (part I)
level_params = dict()
level_params['restol'] = 1e-08
# initialize sweeper parameters (part I)
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = comm.Get_size()
sweeper_params['comm'] = comm
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 100
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
# set up list of Q-delta types and setups
qd_list = ['IEpar', 'Qpar', 'MIN', 'MIN3', 'MIN_GT']
setup_list = [
('heat', 63, [10.0**i for i in range(-3, 3)]),
('advection', 64, [10.0**i for i in range(-3, 3)]),
('vanderpol', 2, [0.1 * 2**i for i in range(0, 10)]),
('fisher', 63, [2**i for i in range(-2, 3)]),
]
# setup_list = [('fisher', 63, [2 * i for i in range(1, 6)])]
# pre-fill results with lists of setups
results = dict()
for setup, nvars, param_list in setup_list:
results[setup] = (nvars, param_list)
# loop over all Q-delta matrix types
for qd_type in qd_list:
# assign implicit Q-delta matrix
sweeper_params['QI'] = qd_type
# loop over all setups
for setup, nvars, param_list in setup_list:
# initialize problem parameters (part I)
problem_params = dict()
if setup != 'vanderpol':
problem_params['nvars'] = nvars # number of degrees of freedom for each level
# loop over all parameters
for param in param_list:
# fill description for the controller
description = dict()
description['sweeper_class'] = generic_implicit_MPI # pass sweeper
description['sweeper_params'] = sweeper_params # pass sweeper parameters
description['step_params'] = step_params # pass step parameters
# description['base_transfer_class'] = base_transfer_mpi
print('working on: %s - %s - %s' % (qd_type, setup, param))
# decide which setup to take
if setup == 'heat':
problem_params['nu'] = param
problem_params['freq'] = 2
problem_params['bc'] = 'dirichlet-zero' # boundary conditions
level_params['dt'] = 0.1
description['problem_class'] = heatNd_unforced
description['problem_params'] = problem_params
description['level_params'] = level_params # pass level parameters
elif setup == 'advection':
problem_params['c'] = param
problem_params['order'] = 2
problem_params['freq'] = 2
problem_params['stencil_type'] = 'center' # boundary conditions
problem_params['bc'] = 'periodic' # boundary conditions
level_params['dt'] = 0.1
description['problem_class'] = advectionNd
description['problem_params'] = problem_params
description['level_params'] = level_params # pass level parameters
elif setup == 'vanderpol':
problem_params['newton_tol'] = 1e-09
problem_params['newton_maxiter'] = 20
problem_params['mu'] = param
problem_params['u0'] = np.array([2.0, 0])
level_params['dt'] = 0.1
description['problem_class'] = vanderpol
description['problem_params'] = problem_params
description['level_params'] = level_params
elif setup == 'fisher':
problem_params['nu'] = 1
problem_params['lambda0'] = param
problem_params['newton_maxiter'] = 20
problem_params['newton_tol'] = 1e-10
problem_params['interval'] = (-5, 5)
level_params['dt'] = 0.01
description['problem_class'] = generalized_fisher
description['problem_params'] = problem_params
description['level_params'] = level_params
else:
print('Setup not implemented..', setup)
exit()
# instantiate controller
controller = controller_nonMPI(
num_procs=1, controller_params=controller_params, description=description
)
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=0, Tend=level_params['dt'])
# filter statistics by type (number of iterations)
iter_counts = get_sorted(stats, type='niter', sortby='time')
# just one time-step, grep number of iteration and store
niter = iter_counts[0][1]
id = ID(setup=setup, qd_type=qd_type, param=param)
results[id] = niter
assert len(results) == (6 + 6 + 10 + 5) * 5 + 4, 'ERROR: did not get all results, got %s' % len(results)
if comm.Get_rank() == 0:
# write out for later visualization
with open('data/parallelSDC_iterations_precond_MPI.pkl', 'wb') as file:
pickle.dump(results, file)
assert os.path.isfile('data/parallelSDC_iterations_precond_MPI.pkl'), 'ERROR: pickle did not create file'
# pragma: no cover
def plot_iterations():
"""
Helper routine to plot iteration counts
"""
with open('data/parallelSDC_iterations_precond_MPI.pkl', 'rb') as file:
results = pickle.load(file)
# find the lists/header required for plotting
qd_type_list = []
setup_list = []
for key in results.keys():
if isinstance(key, ID):
if key.qd_type not in qd_type_list:
qd_type_list.append(key.qd_type)
elif isinstance(key, str):
setup_list.append(key)
print('Found these type of preconditioners:', qd_type_list)
print('Found these setups:', setup_list)
assert len(qd_type_list) == 5, 'ERROR did not find five preconditioners, got %s' % qd_type_list
assert len(setup_list) == 4, 'ERROR: did not find four setup, got %s' % setup_list
plt_helper.setup_mpl()
print('post setup')
# loop over setups and Q-delta types: one figure per setup, all Qds in one plot
for setup in list(setup_list[:]):
plot_setup(results, setup)
mpl.pyplot.close("all")
return 0
def plot_setup(results, setup):
print(f'setup of {setup}')
qd_type_list = ['IEpar', 'Qpar', 'MIN', 'MIN3', 'MIN_GT']
marker_list = ['s', 'o', '^', 'v', 'x']
color_list = ['r', 'g', 'b', 'c', 'm']
fig, ax = plt_helper.newfig(textwidth=238.96, scale=0.89)
for qd_type, marker, color in zip(qd_type_list, marker_list, color_list):
niter = np.zeros(len(results[setup][1]))
for key in results.keys():
if isinstance(key, ID):
if key.setup == setup and key.qd_type == qd_type:
xvalue = results[setup][1].index(key.param)
niter[xvalue] = results[key]
ls = '-'
lw = 1
ax.semilogx(
results[setup][1],
niter,
label=qd_type,
lw=lw,
linestyle=ls,
color=color,
marker=marker,
markeredgecolor='k',
)
if setup == 'heat':
xlabel = r'$\nu$'
elif setup == 'advection':
xlabel = r'$c$'
elif setup == 'fisher':
xlabel = r'$\lambda_0$'
elif setup == 'vanderpol':
xlabel = r'$\mu$'
else:
print('Setup not implemented..', setup)
exit()
ax.set_ylim(0, 60)
fig.legend(loc=2, ncol=1)
ax.set_ylabel('number of iterations')
ax.set_xlabel(xlabel)
ax.grid()
# save plot as PDF and PGF
fname = 'data/parallelSDC_preconditioner_MPI_' + setup
plt_helper.savefig(fname)
del fig, ax
assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
# assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'
print(f"Successfully stored image {fname}.png")
return
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("action", type=str, default="", const="", nargs='?')
args = parser.parse_args()
if args.action == "":
comm = MPI.COMM_WORLD
main(comm=comm)
if comm.Get_rank() == 0:
plot_iterations()
elif args.action == "simulate":
comm = MPI.COMM_WORLD
main(comm=comm)
elif args.action == "plot":
plot_iterations()
else:
raise KeyError(f"Unknown action '{args.action}'. Known actions are 'simulate', 'plot', or none for both")
Results:
Simplified Newton for nonlinear problems¶
The main idea here is to work with a diagonalization of the Q matrix.
While this works well for non-equidistant and non-symmetri nodes like Gauss-Radau, this can only be applied for linear problem, where space and time is separated via Kronecker products.
In order to apply this also for nonlinear problems, we apply an outer Newton iteration to the nonlinear collocation problem and use the diagonalized SDC approach for the linear problem.
Yet, the naive implementation still does not decouple space and time, so that we need to fix the Jacobian at e.g. node 0.
This example compares the iteration counts and errors for this idea (incl. a modified Newton where the Jacobian is not fixed but the approach is applied nonetheless).
Three new sweepers are used here: linearized_implicit_parallel, linearized_implicit_fixed_parallel and linearized_implicit_fixed_parallel_prec.
This part also contains the code newton_vs_sdc.py where simplified and inexact Newton are compared to standard SDC for the generalized Fisher’s equation.
Full code: pySDC/projects/parallelSDC/nonlinear_playground.py
import os
import pickle
import numpy as np
import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.sweeper_classes.generic_implicit import generic_implicit
from pySDC.projects.parallelSDC.GeneralizedFisher_1D_FD_implicit_Jac import generalized_fisher_jac
from pySDC.projects.parallelSDC.linearized_implicit_fixed_parallel import linearized_implicit_fixed_parallel
from pySDC.projects.parallelSDC.linearized_implicit_fixed_parallel_prec import linearized_implicit_fixed_parallel_prec
from pySDC.projects.parallelSDC.linearized_implicit_parallel import linearized_implicit_parallel
def main():
# initialize level parameters
level_params = dict()
level_params['restol'] = 1e-10
level_params['dt'] = 0.01
# This comes as read-in for the step class (this is optional!)
step_params = dict()
step_params['maxiter'] = 50
# This comes as read-in for the problem class
problem_params = dict()
problem_params['nu'] = 1
problem_params['nvars'] = 255
problem_params['lambda0'] = 5.0
problem_params['newton_maxiter'] = 50
problem_params['newton_tol'] = 1e-12
problem_params['interval'] = (-5, 5)
# This comes as read-in for the sweeper class
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = 5
sweeper_params['QI'] = 'LU'
sweeper_params['fixed_time_in_jacobian'] = 0
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
# Fill description dictionary for easy hierarchy creation
description = dict()
description['problem_class'] = generalized_fisher_jac
description['problem_params'] = problem_params
description['sweeper_params'] = sweeper_params
description['level_params'] = level_params
description['step_params'] = step_params
sweeper_list = [
generic_implicit,
linearized_implicit_fixed_parallel_prec,
linearized_implicit_fixed_parallel,
linearized_implicit_parallel,
]
f = open('data/parallelSDC_nonlinear_out.txt', 'w')
uinit = None
uex = None
uend = None
P = None
# loop over the different sweepers and check results
for sweeper in sweeper_list:
description['sweeper_class'] = sweeper
# instantiate the controller
controller = controller_nonMPI(num_procs=1, controller_params=controller_params, description=description)
# setup parameters "in time"
t0 = 0
Tend = 0.1
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(t0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)
# compute exact solution and compare
uex = P.u_exact(Tend)
err = abs(uex - uend)
print('error at time %s: %s' % (Tend, err))
# filter statistics by type (number of iterations)
iter_counts = get_sorted(stats, type='niter', sortby='time')
# compute and print statistics
niters = np.array([item[1] for item in iter_counts])
out = ' Mean number of iterations: %4.2f' % np.mean(niters)
f.write(out + '\n')
print(out)
out = ' Range of values for number of iterations: %2i ' % np.ptp(niters)
f.write(out + '\n')
print(out)
out = ' Position of max/min number of iterations: %2i -- %2i' % (
int(np.argmax(niters)),
int(np.argmin(niters)),
)
f.write(out + '\n')
print(out)
out = ' Std and var for number of iterations: %4.2f -- %4.2f' % (float(np.std(niters)), float(np.var(niters)))
f.write(out + '\n')
f.write(out + '\n')
print(out)
f.write('\n')
print()
assert err < 3.686e-05, 'ERROR: error is too high for sweeper %s, got %s' % (sweeper.__name__, err)
assert (
np.mean(niters) == 7.5 or np.mean(niters) == 4.0
), 'ERROR: mean number of iterations not as expected, got %s' % np.mean(niters)
f.close()
results = dict()
results['interval'] = problem_params['interval']
results['xvalues'] = np.array([(i + 1 - (P.nvars + 1) / 2) * P.dx for i in range(P.nvars)])
results['uinit'] = uinit
results['uend'] = uend
results['uex'] = uex
# write out for later visualization
file = open('data/parallelSDC_results_graphs.pkl', 'wb')
pickle.dump(results, file)
assert os.path.isfile('data/parallelSDC_results_graphs.pkl'), 'ERROR: pickle did not create file'
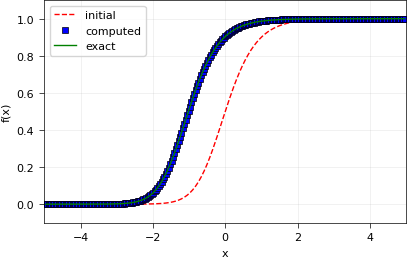
def plot_graphs():
"""
Helper function to plot graphs of initial and final values
"""
file = open('data/parallelSDC_results_graphs.pkl', 'rb')
results = pickle.load(file)
interval = results['interval']
xvalues = results['xvalues']
uinit = results['uinit']
uend = results['uend']
uex = results['uex']
plt_helper.setup_mpl()
# set up figure
plt_helper.newfig(textwidth=338.0, scale=1.0)
plt_helper.plt.xlabel('x')
plt_helper.plt.ylabel('f(x)')
plt_helper.plt.xlim((interval[0] - 0.01, interval[1] + 0.01))
plt_helper.plt.ylim((-0.1, 1.1))
plt_helper.plt.grid()
# plot
plt_helper.plt.plot(xvalues, uinit, 'r--', lw=1, label='initial')
plt_helper.plt.plot(xvalues, uend, 'bs', lw=1, markeredgecolor='k', label='computed')
plt_helper.plt.plot(xvalues, uex, 'g-', lw=1, label='exact')
plt_helper.plt.legend(loc=2, ncol=1)
# save plot as PDF, beautify
fname = 'data/parallelSDC_fisher'
plt_helper.savefig(fname)
assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
# assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'
if __name__ == "__main__":
# main()
plot_graphs()
Results:
Mean number of iterations: 7.50
Range of values for number of iterations: 1
Position of max/min number of iterations: 0 -- 5
Std and var for number of iterations: 0.50 -- 0.25
Std and var for number of iterations: 0.50 -- 0.25
Mean number of iterations: 7.50
Range of values for number of iterations: 1
Position of max/min number of iterations: 0 -- 5
Std and var for number of iterations: 0.50 -- 0.25
Std and var for number of iterations: 0.50 -- 0.25
Mean number of iterations: 4.00
Range of values for number of iterations: 0
Position of max/min number of iterations: 0 -- 0
Std and var for number of iterations: 0.00 -- 0.00
Std and var for number of iterations: 0.00 -- 0.00
Mean number of iterations: 7.50
Range of values for number of iterations: 1
Position of max/min number of iterations: 0 -- 5
Std and var for number of iterations: 0.50 -- 0.25
Std and var for number of iterations: 0.50 -- 0.25
Results:
Full code: pySDC/projects/parallelSDC/newton_vs_sdc.py
import os
import pickle
import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.sweeper_classes.generic_implicit import generic_implicit
from pySDC.projects.parallelSDC.ErrReductionHook import err_reduction_hook
from pySDC.projects.parallelSDC.GeneralizedFisher_1D_FD_implicit_Jac import generalized_fisher_jac
from pySDC.projects.parallelSDC.linearized_implicit_fixed_parallel import linearized_implicit_fixed_parallel
from pySDC.projects.parallelSDC.linearized_implicit_fixed_parallel_prec import linearized_implicit_fixed_parallel_prec
def main():
# initialize level parameters
level_params = dict()
level_params['restol'] = 1e-12
# This comes as read-in for the step class (this is optional!)
step_params = dict()
step_params['maxiter'] = 20
# This comes as read-in for the problem class
problem_params = dict()
problem_params['nu'] = 1
problem_params['nvars'] = 2047
problem_params['lambda0'] = 5.0
problem_params['newton_maxiter'] = 50
problem_params['newton_tol'] = 1e-12
problem_params['interval'] = (-5, 5)
# This comes as read-in for the sweeper class
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = 5
sweeper_params['QI'] = 'LU'
sweeper_params['fixed_time_in_jacobian'] = 0
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
controller_params['hook_class'] = err_reduction_hook
# Fill description dictionary for easy hierarchy creation
description = dict()
description['problem_class'] = generalized_fisher_jac
description['problem_params'] = problem_params
description['sweeper_params'] = sweeper_params
description['step_params'] = step_params
# setup parameters "in time"
t0 = 0
Tend = 0.1
sweeper_list = [generic_implicit, linearized_implicit_fixed_parallel, linearized_implicit_fixed_parallel_prec]
dt_list = [Tend / 2**i for i in range(1, 5)]
results = dict()
results['sweeper_list'] = [sweeper.__name__ for sweeper in sweeper_list]
results['dt_list'] = dt_list
# loop over the different sweepers and check results
for sweeper in sweeper_list:
description['sweeper_class'] = sweeper
error_reduction = []
for dt in dt_list:
print('Working with sweeper %s and dt = %s...' % (sweeper.__name__, dt))
level_params['dt'] = dt
description['level_params'] = level_params
# instantiate the controller
controller = controller_nonMPI(num_procs=1, controller_params=controller_params, description=description)
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(t0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)
# filter statistics
error_pre = get_sorted(stats, type='error_pre_iteration', sortby='iter')[0][1]
error_post = get_sorted(stats, type='error_post_iteration', sortby='iter')[0][1]
error_reduction.append(error_post / error_pre)
print('error and reduction rate at time %s: %6.4e -- %6.4e' % (Tend, error_post, error_reduction[-1]))
results[sweeper.__name__] = error_reduction
print()
file = open('data/error_reduction_data.pkl', 'wb')
pickle.dump(results, file)
file.close()
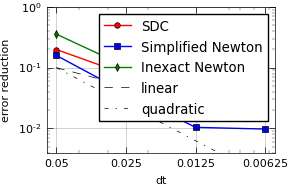
def plot_graphs(cwd=''):
"""
Helper function to plot graphs of initial and final values
Args:
cwd (str): current working directory
"""
plt_helper.mpl.style.use('classic')
file = open(cwd + 'data/error_reduction_data.pkl', 'rb')
results = pickle.load(file)
sweeper_list = results['sweeper_list']
dt_list = results['dt_list']
color_list = ['red', 'blue', 'green']
marker_list = ['o', 's', 'd']
label_list = []
for sweeper in sweeper_list:
if sweeper == 'generic_implicit':
label_list.append('SDC')
elif sweeper == 'linearized_implicit_fixed_parallel':
label_list.append('Simplified Newton')
elif sweeper == 'linearized_implicit_fixed_parallel_prec':
label_list.append('Inexact Newton')
setups = zip(sweeper_list, color_list, marker_list, label_list)
plt_helper.setup_mpl()
plt_helper.newfig(textwidth=238.96, scale=0.89)
for sweeper, color, marker, label in setups:
plt_helper.plt.loglog(
dt_list, results[sweeper], lw=1, ls='-', color=color, marker=marker, markeredgecolor='k', label=label
)
plt_helper.plt.loglog(dt_list, [dt * 2 for dt in dt_list], lw=0.5, ls='--', color='k', label='linear')
plt_helper.plt.loglog(
dt_list, [dt * dt / dt_list[0] * 2 for dt in dt_list], lw=0.5, ls='-.', color='k', label='quadratic'
)
plt_helper.plt.xlabel('dt')
plt_helper.plt.ylabel('error reduction')
plt_helper.plt.grid()
# ax.set_xticks(dt_list, dt_list)
plt_helper.plt.xticks(dt_list, dt_list)
plt_helper.plt.legend(loc=1, ncol=1)
plt_helper.plt.gca().invert_xaxis()
plt_helper.plt.xlim([dt_list[0] * 1.1, dt_list[-1] / 1.1])
plt_helper.plt.ylim([4e-03, 1e0])
# save plot, beautify
fname = 'data/parallelSDC_fisher_newton'
plt_helper.savefig(fname)
assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
# assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'
if __name__ == "__main__":
# main()
plot_graphs()
Results:
Node-parallel SDC with MPI¶
The project also contains a sweeper (and a transfer class) to allow real, MPI-based parallelism of diagonal preconditioners.
We test again the aforementioned ideas, but now add the MIN3 approach: These values have been obtained using Indie Solver,
a commercial solver for black-box optimization which aggregates several state-of-the-art optimization methods (free academic subscription plan).
The objective function in this case is the sum over 17^2 values of lamdt, real and imaginary. This works surprisingly well!
Full code: pySDC/projects/parallelSDC/preconditioner_playground_MPI.py
import os
import pickle
from collections import namedtuple
import numpy as np
from mpi4py import MPI
import argparse
import matplotlib as mpl
mpl.use("Agg")
import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted
from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.AdvectionEquation_ND_FD import advectionNd
from pySDC.implementations.problem_classes.GeneralizedFisher_1D_FD_implicit import generalized_fisher
from pySDC.implementations.problem_classes.HeatEquation_ND_FD import heatNd_unforced
from pySDC.implementations.problem_classes.Van_der_Pol_implicit import vanderpol
from pySDC.implementations.sweeper_classes.generic_implicit_MPI import generic_implicit_MPI
ID = namedtuple('ID', ['setup', 'qd_type', 'param'])
def main(comm=None):
# initialize level parameters (part I)
level_params = dict()
level_params['restol'] = 1e-08
# initialize sweeper parameters (part I)
sweeper_params = dict()
sweeper_params['quad_type'] = 'RADAU-RIGHT'
sweeper_params['num_nodes'] = comm.Get_size()
sweeper_params['comm'] = comm
# initialize step parameters
step_params = dict()
step_params['maxiter'] = 100
# initialize controller parameters
controller_params = dict()
controller_params['logger_level'] = 30
# set up list of Q-delta types and setups
qd_list = ['IEpar', 'Qpar', 'MIN', 'MIN3', 'MIN_GT']
setup_list = [
('heat', 63, [10.0**i for i in range(-3, 3)]),
('advection', 64, [10.0**i for i in range(-3, 3)]),
('vanderpol', 2, [0.1 * 2**i for i in range(0, 10)]),
('fisher', 63, [2**i for i in range(-2, 3)]),
]
# setup_list = [('fisher', 63, [2 * i for i in range(1, 6)])]
# pre-fill results with lists of setups
results = dict()
for setup, nvars, param_list in setup_list:
results[setup] = (nvars, param_list)
# loop over all Q-delta matrix types
for qd_type in qd_list:
# assign implicit Q-delta matrix
sweeper_params['QI'] = qd_type
# loop over all setups
for setup, nvars, param_list in setup_list:
# initialize problem parameters (part I)
problem_params = dict()
if setup != 'vanderpol':
problem_params['nvars'] = nvars # number of degrees of freedom for each level
# loop over all parameters
for param in param_list:
# fill description for the controller
description = dict()
description['sweeper_class'] = generic_implicit_MPI # pass sweeper
description['sweeper_params'] = sweeper_params # pass sweeper parameters
description['step_params'] = step_params # pass step parameters
# description['base_transfer_class'] = base_transfer_mpi
print('working on: %s - %s - %s' % (qd_type, setup, param))
# decide which setup to take
if setup == 'heat':
problem_params['nu'] = param
problem_params['freq'] = 2
problem_params['bc'] = 'dirichlet-zero' # boundary conditions
level_params['dt'] = 0.1
description['problem_class'] = heatNd_unforced
description['problem_params'] = problem_params
description['level_params'] = level_params # pass level parameters
elif setup == 'advection':
problem_params['c'] = param
problem_params['order'] = 2
problem_params['freq'] = 2
problem_params['stencil_type'] = 'center' # boundary conditions
problem_params['bc'] = 'periodic' # boundary conditions
level_params['dt'] = 0.1
description['problem_class'] = advectionNd
description['problem_params'] = problem_params
description['level_params'] = level_params # pass level parameters
elif setup == 'vanderpol':
problem_params['newton_tol'] = 1e-09
problem_params['newton_maxiter'] = 20
problem_params['mu'] = param
problem_params['u0'] = np.array([2.0, 0])
level_params['dt'] = 0.1
description['problem_class'] = vanderpol
description['problem_params'] = problem_params
description['level_params'] = level_params
elif setup == 'fisher':
problem_params['nu'] = 1
problem_params['lambda0'] = param
problem_params['newton_maxiter'] = 20
problem_params['newton_tol'] = 1e-10
problem_params['interval'] = (-5, 5)
level_params['dt'] = 0.01
description['problem_class'] = generalized_fisher
description['problem_params'] = problem_params
description['level_params'] = level_params
else:
print('Setup not implemented..', setup)
exit()
# instantiate controller
controller = controller_nonMPI(
num_procs=1, controller_params=controller_params, description=description
)
# get initial values on finest level
P = controller.MS[0].levels[0].prob
uinit = P.u_exact(0)
# call main function to get things done...
uend, stats = controller.run(u0=uinit, t0=0, Tend=level_params['dt'])
# filter statistics by type (number of iterations)
iter_counts = get_sorted(stats, type='niter', sortby='time')
# just one time-step, grep number of iteration and store
niter = iter_counts[0][1]
id = ID(setup=setup, qd_type=qd_type, param=param)
results[id] = niter
assert len(results) == (6 + 6 + 10 + 5) * 5 + 4, 'ERROR: did not get all results, got %s' % len(results)
if comm.Get_rank() == 0:
# write out for later visualization
with open('data/parallelSDC_iterations_precond_MPI.pkl', 'wb') as file:
pickle.dump(results, file)
assert os.path.isfile('data/parallelSDC_iterations_precond_MPI.pkl'), 'ERROR: pickle did not create file'
# pragma: no cover
def plot_iterations():
"""
Helper routine to plot iteration counts
"""
with open('data/parallelSDC_iterations_precond_MPI.pkl', 'rb') as file:
results = pickle.load(file)
# find the lists/header required for plotting
qd_type_list = []
setup_list = []
for key in results.keys():
if isinstance(key, ID):
if key.qd_type not in qd_type_list:
qd_type_list.append(key.qd_type)
elif isinstance(key, str):
setup_list.append(key)
print('Found these type of preconditioners:', qd_type_list)
print('Found these setups:', setup_list)
assert len(qd_type_list) == 5, 'ERROR did not find five preconditioners, got %s' % qd_type_list
assert len(setup_list) == 4, 'ERROR: did not find four setup, got %s' % setup_list
plt_helper.setup_mpl()
print('post setup')
# loop over setups and Q-delta types: one figure per setup, all Qds in one plot
for setup in list(setup_list[:]):
plot_setup(results, setup)
mpl.pyplot.close("all")
return 0
def plot_setup(results, setup):
print(f'setup of {setup}')
qd_type_list = ['IEpar', 'Qpar', 'MIN', 'MIN3', 'MIN_GT']
marker_list = ['s', 'o', '^', 'v', 'x']
color_list = ['r', 'g', 'b', 'c', 'm']
fig, ax = plt_helper.newfig(textwidth=238.96, scale=0.89)
for qd_type, marker, color in zip(qd_type_list, marker_list, color_list):
niter = np.zeros(len(results[setup][1]))
for key in results.keys():
if isinstance(key, ID):
if key.setup == setup and key.qd_type == qd_type:
xvalue = results[setup][1].index(key.param)
niter[xvalue] = results[key]
ls = '-'
lw = 1
ax.semilogx(
results[setup][1],
niter,
label=qd_type,
lw=lw,
linestyle=ls,
color=color,
marker=marker,
markeredgecolor='k',
)
if setup == 'heat':
xlabel = r'$\nu$'
elif setup == 'advection':
xlabel = r'$c$'
elif setup == 'fisher':
xlabel = r'$\lambda_0$'
elif setup == 'vanderpol':
xlabel = r'$\mu$'
else:
print('Setup not implemented..', setup)
exit()
ax.set_ylim(0, 60)
fig.legend(loc=2, ncol=1)
ax.set_ylabel('number of iterations')
ax.set_xlabel(xlabel)
ax.grid()
# save plot as PDF and PGF
fname = 'data/parallelSDC_preconditioner_MPI_' + setup
plt_helper.savefig(fname)
del fig, ax
assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
# assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'
print(f"Successfully stored image {fname}.png")
return
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("action", type=str, default="", const="", nargs='?')
args = parser.parse_args()
if args.action == "":
comm = MPI.COMM_WORLD
main(comm=comm)
if comm.Get_rank() == 0:
plot_iterations()
elif args.action == "simulate":
comm = MPI.COMM_WORLD
main(comm=comm)
elif args.action == "plot":
plot_iterations()
else:
raise KeyError(f"Unknown action '{args.action}'. Known actions are 'simulate', 'plot', or none for both")
Results:



