The Parareal Algorithm in PalMod
In high-performance computing facilities, the number of cores has increased rapidly in the last years, and will do so further in the future. In contrast, the speed of each single core does not grow any more. Thus, the exploitation of parallelism becomes a crucial point in every design of simulation software where high computational effort is needed. This naturally refers to climate simulations, may these be predictions or paleo runs as in PalMod.
The setting in paleo-computing is special because of two facts: At first, the spatial resolution is numerically coupled with the time-step due to stability conditions. Secondly, the needed long time horizons prohibit short time-steps, and thus restrict also the spatial resolution. As a result, the high number of available cores cannot be used to reduce the overall computation time. They may nevertheless be used to perform parallel ensemble and sensitivity experiments.
The concept of time-parallelism allows to exploit more and more hardware cores. It breaks the intuitively clear and familiar concept of a “serial” time: Here steps in the algorithm only partly reflect an actual step from one time instant to another. Contrarily, the steps of a parallel-in-time algorithm are internal steps on the way towards the final solution, which gives a continuous trajectory at the end of the computation. In several research papers, it can already be seen that also problems with different internal time scales or including chaotic behavior (e.g. the Lorenz system) can be treated with this method.
However, applying a parallel-in-time method to the PalMod setting still is a challenge, since it has to be implemented using the available Earth System Models. Here, several options are thinkable: Coupling between different spatial resolutions as well as the usage of simpler reduced or intermediate complexity models. In this context, the parareal method is a mathematical key enabler for faster climate simulations and with this perfectly fits to the ambitious goal of the PalMod project. Currently the parareal method is implemented in the simulation environment of PalMod’s Work Package 4.3. In PalMod, we make use of the Micro-Macro Parareal approach, in cooperation with G. Samaey, KU Leuven: In this version of Parareal [1] , the coarse propagator in the Paraeal setting is a model with a different structure. This can be a simpler model.
In our first example, the coarse model is a zero-dimensional so-called Energy Balance Model (EBM). This model is based on the balance of incoming and outgoing for the whole Earth as 0-D point in space. The only state variable is the global mean temperature. The original, fine model in the Micro-Macro setting is based on the same modeling principles, but spatially one-dimensional. Additional lifting and averaging operators have to be constructed for the algorithm:
- To obtain the initial values for the fine model on each subinterval, the coarse output has to be lifted to the fine resolution.
- To compute the jumps, the fine output has to be restricted/averaged.
By now, simplified model examples have been tested with Parareal in PalMod:
- 0-d and 1-d EBMs (see Figure 1 for convergence results)
- 2-d rotating shallow water equations
- Coupled 2-d ocean and EBM with reduced order model for ocean.
Candidates for the PalMod project are:
- Different resolutions of Earth System Models (ESMs)
- Earth System Models of Intermediate Complexity (EMICs) as coarse model
- Newly constructed reduced order models as coarse models
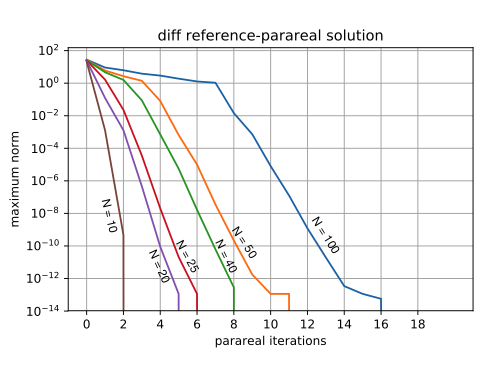
Figure 1 Convergence of micro-macro parareal method for 0-D/1-D nonlinear Energy Balance Model and different numbers N of parareal subintervals.
- F. Legoll, T. Lelièvre, and G. Samaey, “A Micro-Macro Parareal Algorithm: Application to Singularly Perturbed Ordinary Differential Equations,” SIAM Journal on Scientific Computing, vol. 35, no. 4, pp. A1951–A1986, 2013, doi: 10.1137/120872681. [Online]. Available at: http://dx.doi.org/10.1137/120872681