Asymptotic convergence of PFASST

This project investigates the impact of the convergence results described in the paper “Asymptotic convergence of PFASST for linear problems”. We use 1D heat equation and advection equation to show how PFASST converges in the stiff as well as in the non-stiff limit. Note that due to the long runtime, not all results are generated via CI.

Organisation of the project

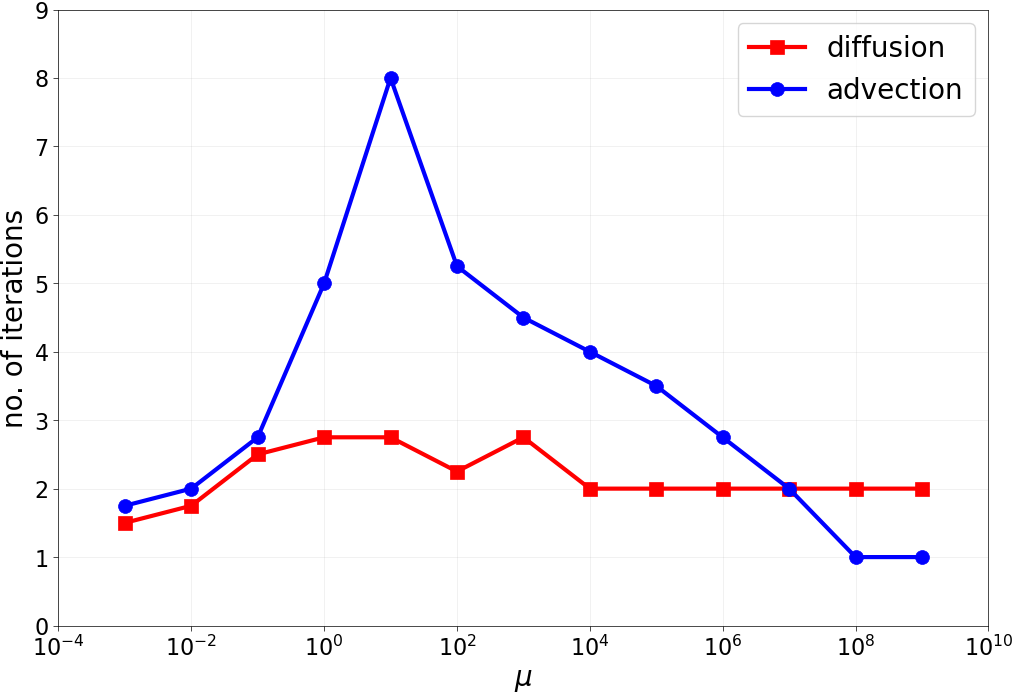
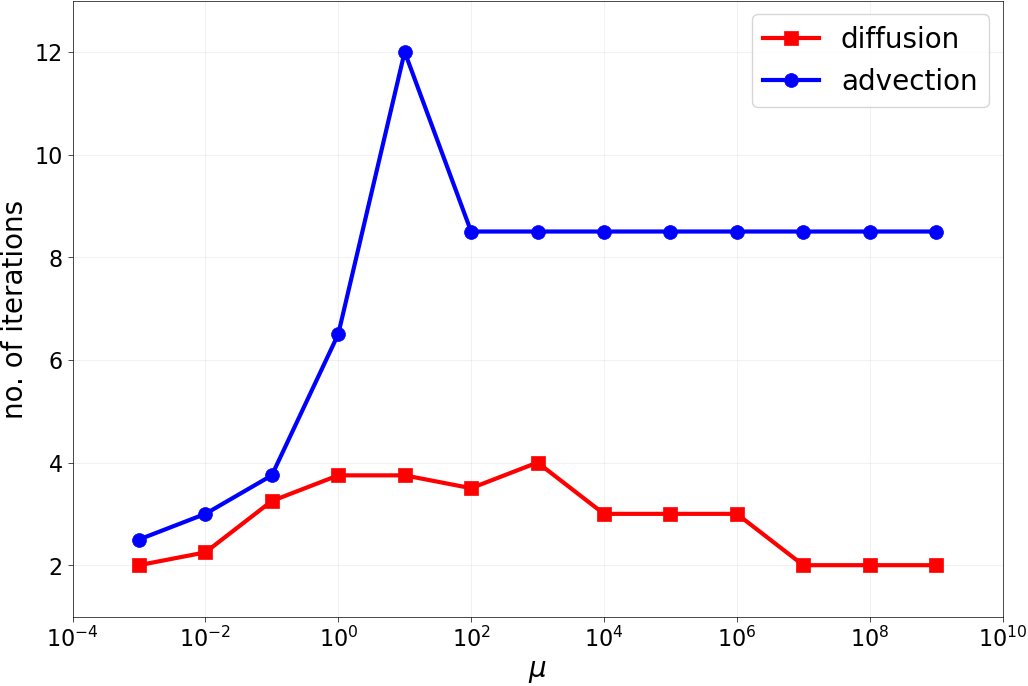
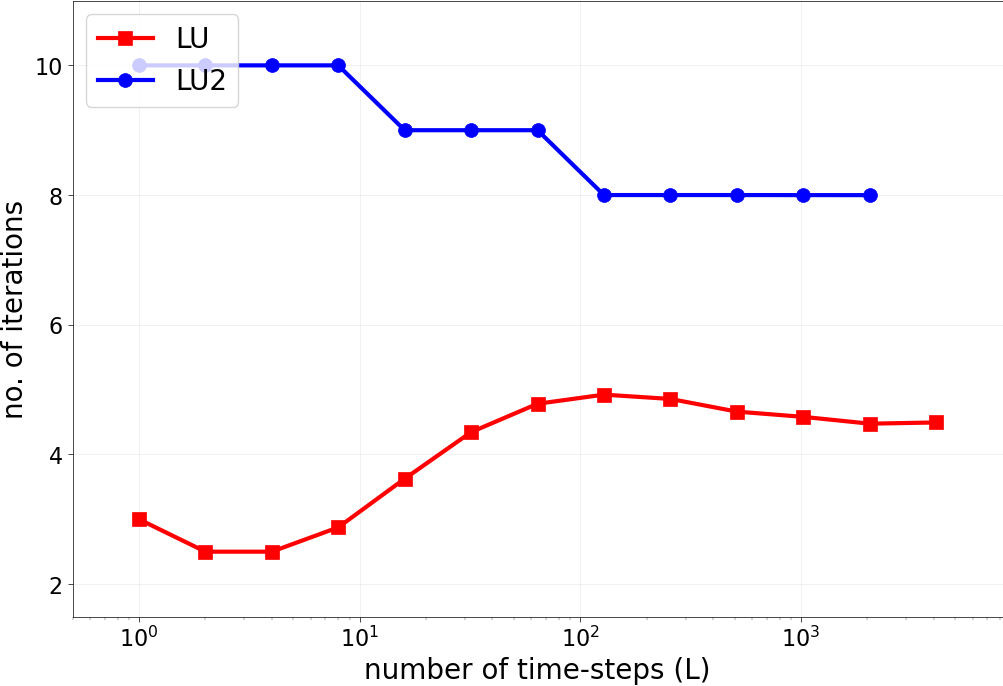
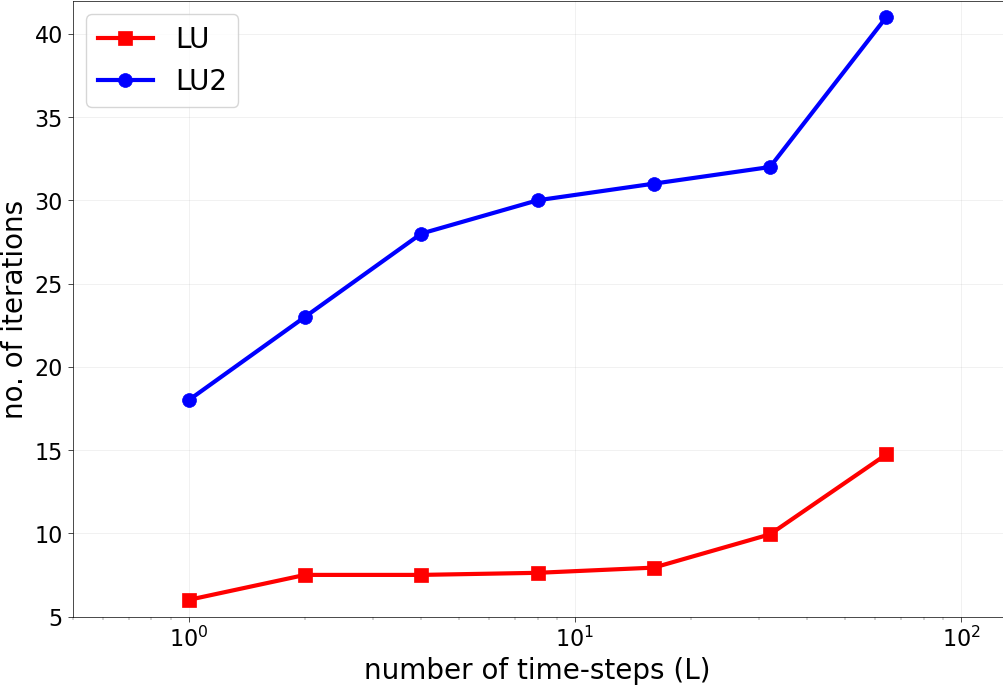
• conv_test_to0.py and conv_test_toinf.py: plots spectral radius of the smoother’s iteration matrix for different eigenvalues. See Figures 1 and 2 in the paper.

• smoother_specrad_heatmap.py: generates heatmap of the spectral radius of the smoother’s iteration matrix for different eigenvalues in the test equation. See Figure 3.

• PFASST_conv_tests.py and PFASST_conv_Linf.py: runs PFASST for advection and diffusion checking teh iteration counts until convergence. See Figures 4 and 5 and below.

Results: