Compression in pySDC

This project aims to implement compression in pySDC in whatever way proves to be useful. It is a collaboration between Clemson University, Argonne National Laboratory and Forschungszentrum Juelich under the umbrella of JLESC. See the project web page here.

Introduction

PDE solvers provide ample opportunity for compression to improve certain aspects of the code. See for instance Sebastian Goetschel’s and Martin Weiser’s nice review on the topic.

Due to current hardware trends, codes are often memory bound rather than compute bound, which means computational resources are perhaps more wisely spent on compression such that memory access can be reduced and more performance can be leveraged. This applies, in particular, to distributed systems where interconnect speeds are yet slower than memory access speeds. As PinT algorithms target large scale distributed systems because concurrency in the time direction usually comes with lower parallel efficiency than in the space direction and is hence best implemented on top of spatial parallelism, it is an ideal candidate to benefit from compression.

SDC, in particular, is a collocation method, which approximates the integral in time by a weighted sum of right hand side evaluations at intermediate time points (collocation nodes). All of these need to be available in memory during the sweeps where the solutions at the collocation nodes are updated. For PDEs, this can be substantial in size and the algorithm could benefit greatly from compressing these data. As right hand side evaluations at individual collocation nodes are required during the sweeps, they either need to be compressed separately, or random access needs to be maintained.

In parallel computation based on decomposition of the domain, the interface needs to be communicated between processors. For PinT, this interface corresponds to the solution of the time step allotted to a process, which becomes the initial conditions for the next process. As this is a large object, communication can become expensive and compressed communication can speed this up.

We are also interested in compression with respect to resilience. For instance, we introduce inexactness during lossy compression, which provides significantly greater compression factors than lossless compression, and we want to be able to answer the question of how large of an inexactness we can afford while maintaining the accuracy we desire from the final outcome. This is interesting for algorithms detecting soft faults. Picture SDC in an early iteration, where the solution is not yet converged and a soft fault occurs. A resilient algorithm might trigger a costly restart which is unnecessary as the impact of the soft fault may not be noticeable in the converged solution.

Opportunities for compression to be useful in PDE solvers are endless. We will see how the project progresses and update this page accordingly.

Methods

Since pySDC is a prototyping library, it provides a good playground to easily implement compression. However, we may not be able to measure a reduction in memory footprint due to Python’s memory management.

For compression, we use the libpressio library maintained by Robert Underwood at Argonne National Laboratory. As a starting point we use the SZ3 compressor. We use a docker container with an installation of libpressio and pySDC working together. See the guide on how to use the container.

Proof of Concept

For a proof of concept, we take the solution and right hand sides and compress and immediately decompress them every time they get updated during the sweeps. While this provides no benefit, it should capture the downsides of compression. We measure the local order of accuracy in time and verify that it increases by one with each sweep for an advection problem. While the order is typically only maintained up to machine precision or the discretization error, we find now that accuracy now stalls at the error bound that we set for the compressor. See below for corresponding figures, where the difference between the colored lines is the number of SDC iterations and the dashed line marks the error bound for SZ3.

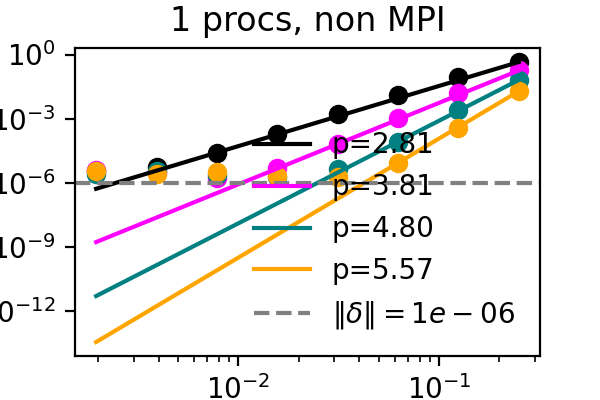
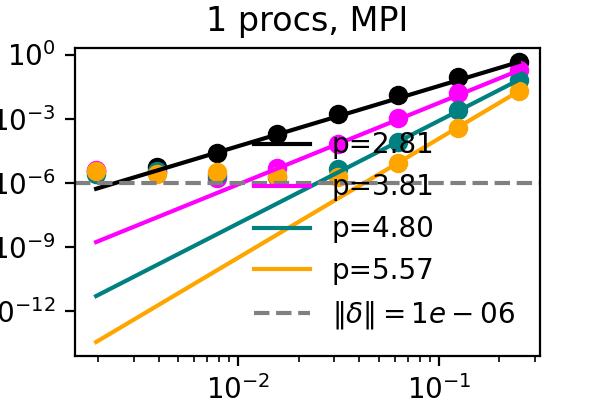
It has recently been demonstrated that the small scale PinT algorithm Block Gauss Seidel SDC maintains the order of single step SDC, so we can repeat the same test but with multiple processors, each with their own time step to solve:

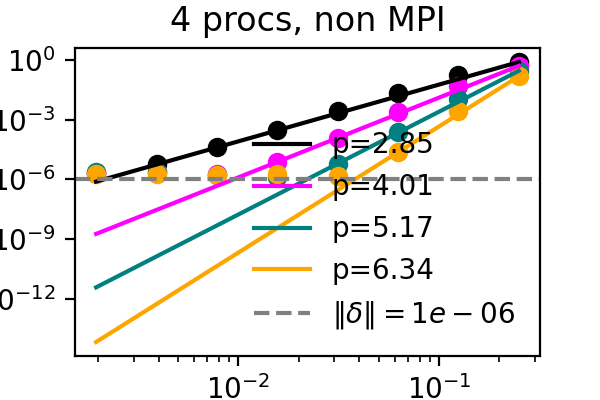
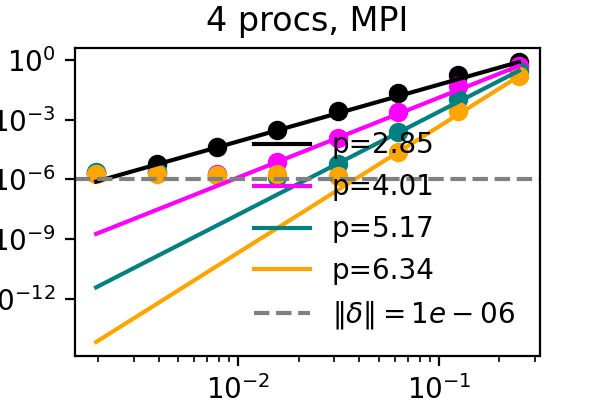
The above plots showcase that both time-serial SDC as well as time-parallel Block Gauss-Seidel SDC do not suffer from compression when the compression error bound is below other numerical errors and that both the MPI and simulated parallelism versions work. After establishing that the downsides of compression can be controlled, it remains to apply compression in a manner that is beneficial to the algorithm.