Second-order Problems¶

In this project, we run several examples of the second-order Verlet-SDC integrator. This SDC variant is the core integrator for the Boris method, which we use e.g. in the 3rd tutorial.

Simple problems¶

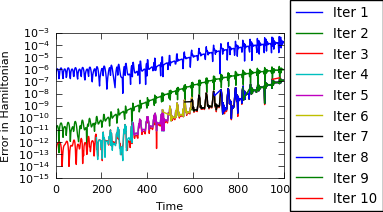
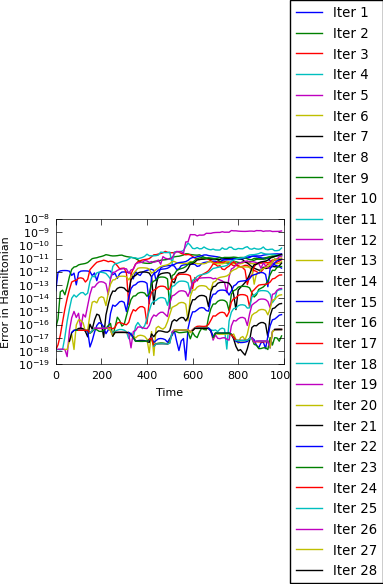
We first test the integrator for some rather simple problems, namely the harmonic oscillator and the Henon-Heiles problem. For both problems we make use of the hook hamiltonian_output to monitor the deviation from the exact Hamiltonian. PFASST is run with 100 processors (virtually parallel) and the deviation from the initial Hamiltonian is shown.

Full code: pySDC/projects/Hamiltonian/simple_problems.py

import os
from collections import defaultdict

import dill
import numpy as np

import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted, filter_stats

from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.HarmonicOscillator import harmonic_oscillator
from pySDC.implementations.problem_classes.HenonHeiles import henon_heiles
from pySDC.implementations.sweeper_classes.verlet import verlet
from pySDC.implementations.transfer_classes.TransferParticles_NoCoarse import particles_to_particles
from pySDC.projects.Hamiltonian.hamiltonian_output import hamiltonian_output


def setup_harmonic():
    """
    Helper routine for setting up everything for the harmonic oscillator

    Returns:
        description (dict): description of the controller
        controller_params (dict): controller parameters
    """

    # initialize level parameters
    level_params = dict()
    level_params['restol'] = 1e-10
    level_params['dt'] = 0.5

    # initialize sweeper parameters
    sweeper_params = dict()
    sweeper_params['quad_type'] = 'LOBATTO'
    sweeper_params['num_nodes'] = [5, 3]
    sweeper_params['initial_guess'] = 'zero'

    # initialize problem parameters for the Penning trap
    problem_params = dict()
    problem_params['k'] = 1.0
    problem_params['phase'] = 0.0
    problem_params['amp'] = 1.0

    # initialize step parameters
    step_params = dict()
    step_params['maxiter'] = 50

    # initialize controller parameters
    controller_params = dict()
    controller_params['hook_class'] = hamiltonian_output  # specialized hook class for more statistics and output
    controller_params['logger_level'] = 30

    # Fill description dictionary for easy hierarchy creation
    description = dict()
    description['problem_class'] = harmonic_oscillator
    description['problem_params'] = problem_params
    description['sweeper_class'] = verlet
    description['sweeper_params'] = sweeper_params
    description['level_params'] = level_params
    description['step_params'] = step_params
    description['space_transfer_class'] = particles_to_particles

    return description, controller_params


def setup_henonheiles():
    """
    Helper routine for setting up everything for the Henon Heiles problem

    Returns:
        description (dict): description of the controller
        controller_params (dict): controller parameters
    """

    # initialize level parameters
    level_params = dict()
    level_params['restol'] = 1e-10
    level_params['dt'] = 0.25

    # initialize sweeper parameters
    sweeper_params = dict()
    sweeper_params['quad_type'] = 'LOBATTO'
    sweeper_params['num_nodes'] = [5, 3]
    sweeper_params['initial_guess'] = 'zero'

    # initialize problem parameters for the Penning trap
    problem_params = dict()

    # initialize step parameters
    step_params = dict()
    step_params['maxiter'] = 50

    # initialize controller parameters
    controller_params = dict()
    controller_params['hook_class'] = hamiltonian_output  # specialized hook class for more statistics and output
    controller_params['logger_level'] = 30

    # Fill description dictionary for easy hierarchy creation
    description = dict()
    description['problem_class'] = henon_heiles
    description['problem_params'] = problem_params
    description['sweeper_class'] = verlet
    description['sweeper_params'] = sweeper_params
    description['level_params'] = level_params
    description['step_params'] = step_params
    description['space_transfer_class'] = particles_to_particles

    return description, controller_params


def run_simulation(prob=None):
    """
    Routine to run the simulation of a second order problem

    Args:
        prob (str): name of the problem

    """

    # check what problem type we have and set up corresponding description and variables
    if prob == 'harmonic':
        description, controller_params = setup_harmonic()
        # set time parameters
        t0 = 0.0
        Tend = 50.0
        num_procs = 100
        maxmeaniter = 6.5
    elif prob == 'henonheiles':
        description, controller_params = setup_henonheiles()
        # set time parameters
        t0 = 0.0
        Tend = 25.0
        num_procs = 100
        maxmeaniter = 5.0
    else:
        raise NotImplementedError('Problem type not implemented, got %s' % prob)

    # instantiate the controller
    controller = controller_nonMPI(num_procs=num_procs, controller_params=controller_params, description=description)

    # get initial values on finest level
    P = controller.MS[0].levels[0].prob
    uinit = P.u_exact(t=t0)

    # call main function to get things done...
    uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)

    # filter statistics by type (number of iterations)
    iter_counts = get_sorted(stats, type='niter', sortby='time')

    # compute and print statistics
    # for item in iter_counts:
    #     out = 'Number of iterations for time %4.2f: %2i' % item
    #     print(out)

    niters = np.array([item[1] for item in iter_counts])
    out = '   Mean number of iterations: %4.2f' % np.mean(niters)
    print(out)
    out = '   Range of values for number of iterations: %2i ' % np.ptp(niters)
    print(out)
    out = '   Position of max/min number of iterations: %2i -- %2i' % (int(np.argmax(niters)), int(np.argmin(niters)))
    print(out)
    out = '   Std and var for number of iterations: %4.2f -- %4.2f' % (float(np.std(niters)), float(np.var(niters)))
    print(out)

    assert np.mean(niters) <= maxmeaniter, 'Mean number of iterations is too high, got %s' % np.mean(niters)

    fname = 'data/' + prob + '.dat'
    f = open(fname, 'wb')
    dill.dump(stats, f)
    f.close()

    assert os.path.isfile(fname), 'Run for %s did not create stats file' % prob


def show_results(prob=None, cwd=''):
    """
    Helper function to plot the error of the Hamiltonian

    Args:
        prob (str): name of the problem
        cwd (str): current working directory
    """

    # read in the dill data
    f = open(cwd + 'data/' + prob + '.dat', 'rb')
    stats = dill.load(f)
    f.close()

    # extract error in hamiltonian and prepare for plotting
    extract_stats = filter_stats(stats, type='err_hamiltonian')
    result = defaultdict(list)
    for k, v in extract_stats.items():
        result[k.iter].append((k.time, v))
    for k, _ in result.items():
        result[k] = sorted(result[k], key=lambda x: x[0])

    plt_helper.mpl.style.use('classic')
    plt_helper.setup_mpl()
    plt_helper.newfig(textwidth=238.96, scale=0.89)

    # Rearrange data for easy plotting
    err_ham = 1
    for k, v in result.items():
        time = [item[0] for item in v]
        ham = [item[1] for item in v]
        err_ham = ham[-1]
        plt_helper.plt.semilogy(time, ham, '-', lw=1, label='Iter ' + str(k))

    assert err_ham < 3.7e-08, 'Error in the Hamiltonian is too large for %s, got %s' % (prob, err_ham)

    plt_helper.plt.xlabel('Time')
    plt_helper.plt.ylabel('Error in Hamiltonian')
    plt_helper.plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

    fname = 'data/' + prob + '_hamiltonian'
    plt_helper.savefig(fname)

    assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
    # assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
    assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'


def main():
    prob = 'harmonic'
    run_simulation(prob)
    show_results(prob)
    prob = 'henonheiles'
    run_simulation(prob)
    show_results(prob)


if __name__ == "__main__":
    main()

Results:

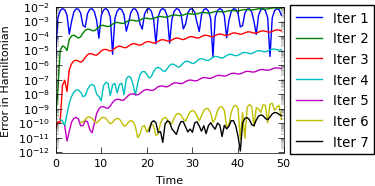
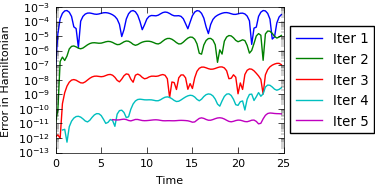
Solar system problem¶

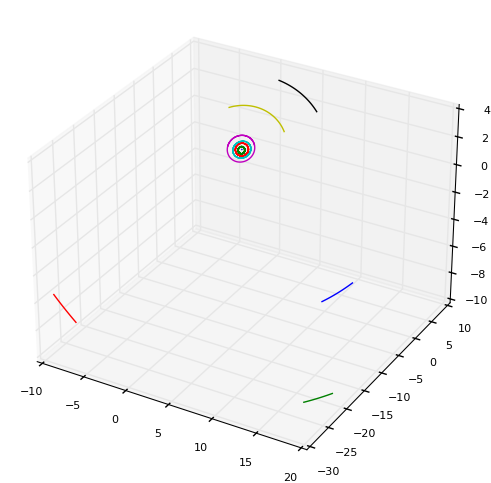
In this slightly more complex setup we simulate the movement of planets in the solar system. The acceleration due to gravitational forces are computed using a simple N^2 solver. We can use two different setups:

OuterSolarSystem problem class: only the six outer planets are simulated, namely the Sun (which in its mass contains the inner planets), Jupiter, Saturn, Uranus, Neptune and Pluto.
FullSolarSystem problem class: all planets are simulated, with earth and moon combined

Coarsening can be done using only the sun for computing the acceleration. Note how PFASST works very well for the outer solar system problem, but not so well for the full solar system problem. Here, over 15 iterations are required in the mean, while SDC and MLSDC require only about 5 per step.

Full code: pySDC/projects/Hamiltonian/solar_system.py

import os
from collections import defaultdict
from mpl_toolkits.mplot3d import Axes3D

import dill
import numpy as np

import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted, filter_stats

from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.FullSolarSystem import full_solar_system
from pySDC.implementations.problem_classes.OuterSolarSystem import outer_solar_system
from pySDC.implementations.sweeper_classes.verlet import verlet
from pySDC.implementations.transfer_classes.TransferParticles_NoCoarse import particles_to_particles
from pySDC.projects.Hamiltonian.hamiltonian_output import hamiltonian_output


def setup_outer_solar_system():
    """
    Helper routine for setting up everything for the outer solar system problem

    Returns:
        description (dict): description of the controller
        controller_params (dict): controller parameters
    """

    # initialize level parameters
    level_params = dict()
    level_params['restol'] = 1e-10
    level_params['dt'] = 100.0

    # initialize sweeper parameters
    sweeper_params = dict()
    sweeper_params['quad_type'] = 'LOBATTO'
    sweeper_params['num_nodes'] = [5, 3]
    sweeper_params['initial_guess'] = 'spread'

    # initialize problem parameters for the Penning trap
    problem_params = dict()
    problem_params['sun_only'] = [False, True]

    # initialize step parameters
    step_params = dict()
    step_params['maxiter'] = 50

    # initialize controller parameters
    controller_params = dict()
    controller_params['hook_class'] = hamiltonian_output  # specialized hook class for more statistics and output
    controller_params['logger_level'] = 30

    # Fill description dictionary for easy hierarchy creation
    description = dict()
    description['problem_class'] = outer_solar_system
    description['problem_params'] = problem_params
    description['sweeper_class'] = verlet
    description['sweeper_params'] = sweeper_params
    description['level_params'] = level_params
    description['step_params'] = step_params
    description['space_transfer_class'] = particles_to_particles

    return description, controller_params


def setup_full_solar_system():
    """
    Helper routine for setting up everything for the full solar system problem

    Returns:
        description (dict): description of the controller
        controller_params (dict): controller parameters
    """

    # initialize level parameters
    level_params = dict()
    level_params['restol'] = 1e-10
    level_params['dt'] = 10.0

    # initialize sweeper parameters
    sweeper_params = dict()
    sweeper_params['quad_type'] = 'LOBATTO'
    sweeper_params['num_nodes'] = [5, 3]
    sweeper_params['initial_guess'] = 'spread'

    # initialize problem parameters for the Penning trap
    problem_params = dict()
    problem_params['sun_only'] = [False, True]

    # initialize step parameters
    step_params = dict()
    step_params['maxiter'] = 50

    # initialize controller parameters
    controller_params = dict()
    controller_params['hook_class'] = hamiltonian_output  # specialized hook class for more statistics and output
    controller_params['logger_level'] = 30

    # Fill description dictionary for easy hierarchy creation
    description = dict()
    description['problem_class'] = full_solar_system
    description['problem_params'] = problem_params
    description['sweeper_class'] = verlet
    description['sweeper_params'] = sweeper_params
    description['level_params'] = level_params
    description['step_params'] = step_params
    description['space_transfer_class'] = particles_to_particles

    return description, controller_params


def run_simulation(prob=None):
    """
    Routine to run the simulation of a second order problem

    Args:
        prob (str): name of the problem

    """

    if prob == 'outer_solar_system':
        description, controller_params = setup_outer_solar_system()
        # set time parameters
        t0 = 0.0
        Tend = 10000.0
        num_procs = 100
        maxmeaniter = 6.0
    elif prob == 'full_solar_system':
        description, controller_params = setup_full_solar_system()
        # set time parameters
        t0 = 0.0
        Tend = 1000.0
        num_procs = 100
        maxmeaniter = 19.0
    else:
        raise NotImplementedError('Problem type not implemented, got %s' % prob)

    f = open('data/' + prob + '_out.txt', 'w')
    out = 'Running ' + prob + ' problem with %s processors...' % num_procs
    f.write(out + '\n')
    print(out)

    # instantiate the controller
    controller = controller_nonMPI(num_procs=num_procs, controller_params=controller_params, description=description)

    # get initial values on finest level
    P = controller.MS[0].levels[0].prob
    uinit = P.u_exact(t=t0)

    # call main function to get things done...
    uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)

    # filter statistics by type (number of iterations)
    iter_counts = get_sorted(stats, type='niter', sortby='time')

    # compute and print statistics
    # for item in iter_counts:
    #     out = 'Number of iterations for time %4.2f: %2i' % item
    #     f.write(out)
    #     print(out)

    niters = np.array([item[1] for item in iter_counts])
    out = '   Mean number of iterations: %4.2f' % np.mean(niters)
    f.write(out + '\n')
    print(out)
    out = '   Range of values for number of iterations: %2i ' % np.ptp(niters)
    f.write(out + '\n')
    print(out)
    out = '   Position of max/min number of iterations: %2i -- %2i' % (int(np.argmax(niters)), int(np.argmin(niters)))
    f.write(out + '\n')
    print(out)
    out = '   Std and var for number of iterations: %4.2f -- %4.2f' % (float(np.std(niters)), float(np.var(niters)))
    f.write(out + '\n')
    print(out)
    f.close()

    assert np.mean(niters) <= maxmeaniter, 'Mean number of iterations is too high, got %s' % np.mean(niters)

    fname = 'data/' + prob + '.dat'
    f = open(fname, 'wb')
    dill.dump(stats, f)
    f.close()

    assert os.path.isfile(fname), 'Run for %s did not create stats file' % prob


def show_results(prob=None, cwd=''):
    """
    Helper function to plot the error of the Hamiltonian

    Args:
        prob (str): name of the problem
        cwd (str): current working directory
    """

    # read in the dill data
    f = open(cwd + 'data/' + prob + '.dat', 'rb')
    stats = dill.load(f)
    f.close()

    plt_helper.mpl.style.use('classic')
    plt_helper.setup_mpl()

    # extract error in hamiltonian and prepare for plotting
    extract_stats = filter_stats(stats, type='err_hamiltonian')
    result = defaultdict(list)
    for k, v in extract_stats.items():
        result[k.iter].append((k.time, v))
    for k, _ in result.items():
        result[k] = sorted(result[k], key=lambda x: x[0])

    plt_helper.newfig(textwidth=238.96, scale=0.89)

    # Rearrange data for easy plotting
    err_ham = 1
    for k, v in result.items():
        time = [item[0] for item in v]
        ham = [item[1] for item in v]
        err_ham = ham[-1]
        plt_helper.plt.semilogy(time, ham, '-', lw=1, label='Iter ' + str(k))
    assert err_ham < 2.4e-14, 'Error in the Hamiltonian is too large for %s, got %s' % (prob, err_ham)

    plt_helper.plt.xlabel('Time')
    plt_helper.plt.ylabel('Error in Hamiltonian')
    plt_helper.plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

    fname = 'data/' + prob + '_hamiltonian'
    plt_helper.savefig(fname)

    assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
    # assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
    assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'

    # extract positions and prepare for plotting
    result = get_sorted(stats, type='position', sortby='time')

    fig = plt_helper.plt.figure()
    ax = fig.add_subplot(111, projection='3d')

    # Rearrange data for easy plotting
    nparts = len(result[1][1][0])
    ndim = len(result[1][1])
    nsteps = len(result)
    pos = np.zeros((nparts, ndim, nsteps))

    for idx, item in enumerate(result):
        for n in range(nparts):
            for m in range(ndim):
                pos[n, m, idx] = item[1][m][n]

    for n in range(nparts):
        if ndim == 2:
            ax.plot(pos[n, 0, :], pos[n, 1, :])
        elif ndim == 3:
            ax.plot(pos[n, 0, :], pos[n, 1, :], pos[n, 2, :])
        else:
            raise NotImplementedError('Wrong number of dimensions for plotting, got %s' % ndim)

    fname = 'data/' + prob + '_positions'
    plt_helper.savefig(fname)

    assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
    # assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
    assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'


def main():
    prob = 'outer_solar_system'
    run_simulation(prob)
    show_results(prob)
    prob = 'full_solar_system'
    run_simulation(prob)
    show_results(prob)


if __name__ == "__main__":
    main()

Results:

Running outer_solar_system problem with 100 processors...
   Mean number of iterations: 5.06
   Range of values for number of iterations:  4 
   Position of max/min number of iterations: 74 --  0
   Std and var for number of iterations: 0.75 -- 0.56

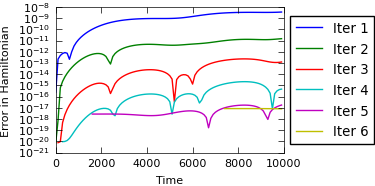
../_images/outer_solar_system_hamiltonian.png

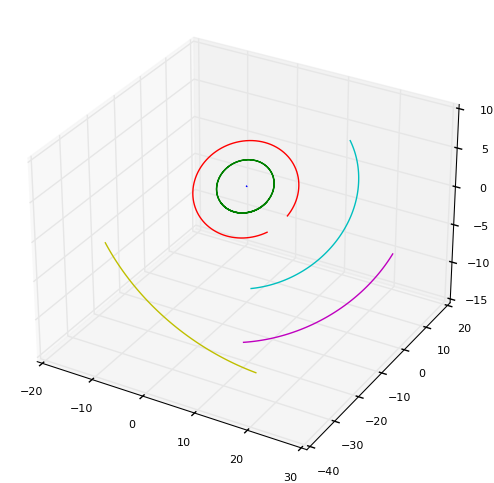
../_images/outer_solar_system_positions.png

Running full_solar_system problem with 100 processors...
   Mean number of iterations: 18.02
   Range of values for number of iterations: 24 
   Position of max/min number of iterations: 96 --  0
   Std and var for number of iterations: 6.37 -- 40.54

../_images/full_solar_system_hamiltonian.png

../_images/full_solar_system_positions.png

Fermi-Pasta-Ulam-Tsingou problem¶

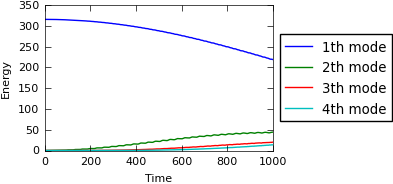
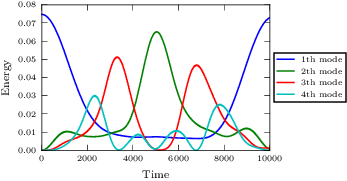
This is the famous FPUT problem, one of the first numerical simulation done in physics. The basis for this setup can be found here and we implement this in the FermiPastaUlamTsingou problem class. Due to time limitations in the CI environment, we only run the first few steps and not until Tend=10000. We refer to the right-most picture below for the full run. Note that we run MLSDC here, since PFASST does not seem to converge easily.

Full code: pySDC/projects/Hamiltonian/fput.py

import os
from collections import defaultdict

import dill
import numpy as np

import pySDC.helpers.plot_helper as plt_helper
from pySDC.helpers.stats_helper import get_sorted, filter_stats

from pySDC.implementations.controller_classes.controller_nonMPI import controller_nonMPI
from pySDC.implementations.problem_classes.FermiPastaUlamTsingou import fermi_pasta_ulam_tsingou
from pySDC.implementations.sweeper_classes.verlet import verlet
from pySDC.implementations.transfer_classes.TransferParticles_NoCoarse import particles_to_particles
from pySDC.projects.Hamiltonian.hamiltonian_and_energy_output import hamiltonian_and_energy_output


def setup_fput():
    """
    Helper routine for setting up everything for the Fermi-Pasta-Ulam-Tsingou problem

    Returns:
        description (dict): description of the controller
        controller_params (dict): controller parameters
    """

    # initialize level parameters
    level_params = dict()
    level_params['restol'] = 1e-12
    level_params['dt'] = 2.0

    # initialize sweeper parameters
    sweeper_params = dict()
    sweeper_params['quad_type'] = 'LOBATTO'
    sweeper_params['num_nodes'] = [5, 3]
    sweeper_params['initial_guess'] = 'zero'

    # initialize problem parameters for the Penning trap
    problem_params = dict()
    problem_params['npart'] = 2048
    problem_params['alpha'] = 0.25
    problem_params['k'] = 1.0
    problem_params['energy_modes'] = [[1, 2, 3, 4]]

    # initialize step parameters
    step_params = dict()
    step_params['maxiter'] = 50

    # initialize controller parameters
    controller_params = dict()
    controller_params['hook_class'] = hamiltonian_and_energy_output
    controller_params['logger_level'] = 30

    # Fill description dictionary for easy hierarchy creation
    description = dict()
    description['problem_class'] = fermi_pasta_ulam_tsingou
    description['problem_params'] = problem_params
    description['sweeper_class'] = verlet
    description['sweeper_params'] = sweeper_params
    description['level_params'] = level_params
    description['step_params'] = step_params
    description['space_transfer_class'] = particles_to_particles

    return description, controller_params


def run_simulation():
    """
    Routine to run the simulation of a second order problem

    """

    description, controller_params = setup_fput()
    # set time parameters
    t0 = 0.0
    # set this to 10000 to reproduce the picture in
    # http://www.scholarpedia.org/article/Fermi-Pasta-Ulam_nonlinear_lattice_oscillations
    Tend = 1000.0
    num_procs = 1

    f = open('data/fput_out.txt', 'w')
    out = 'Running fput problem with %s processors...' % num_procs
    f.write(out + '\n')
    print(out)

    # instantiate the controller
    controller = controller_nonMPI(num_procs=num_procs, controller_params=controller_params, description=description)

    # get initial values on finest level
    P = controller.MS[0].levels[0].prob
    uinit = P.u_exact(t=t0)

    # call main function to get things done...
    uend, stats = controller.run(u0=uinit, t0=t0, Tend=Tend)

    # filter statistics by type (number of iterations)
    iter_counts = get_sorted(stats, type='niter', sortby='time')

    # compute and print statistics
    # for item in iter_counts:
    #     out = 'Number of iterations for time %4.2f: %2i' % item
    #     f.write(out + '\n')
    #     print(out)

    niters = np.array([item[1] for item in iter_counts])
    out = '   Mean number of iterations: %4.2f' % np.mean(niters)
    f.write(out + '\n')
    print(out)
    out = '   Range of values for number of iterations: %2i ' % np.ptp(niters)
    f.write(out + '\n')
    print(out)
    out = '   Position of max/min number of iterations: %2i -- %2i' % (int(np.argmax(niters)), int(np.argmin(niters)))
    f.write(out + '\n')
    print(out)
    out = '   Std and var for number of iterations: %4.2f -- %4.2f' % (float(np.std(niters)), float(np.var(niters)))
    f.write(out + '\n')
    print(out)

    # get runtime
    timing_run = get_sorted(stats, type='timing_run', sortby='time')[0][1]
    out = '... took %6.4f seconds to run this.' % timing_run
    f.write(out + '\n')
    print(out)
    f.close()

    # assert np.mean(niters) <= 3.46, 'Mean number of iterations is too high, got %s' % np.mean(niters)

    fname = 'data/fput.dat'
    f = open(fname, 'wb')
    dill.dump(stats, f)
    f.close()

    assert os.path.isfile(fname), 'Run for %s did not create stats file'


def show_results(cwd=''):
    """
    Helper function to plot the error of the Hamiltonian

    Args:
        cwd (str): current working directory
    """

    # read in the dill data
    f = open(cwd + 'data/fput.dat', 'rb')
    stats = dill.load(f)
    f.close()

    plt_helper.mpl.style.use('classic')
    plt_helper.setup_mpl()

    # HAMILTONIAN PLOTTING #
    # extract error in hamiltonian and prepare for plotting
    extract_stats = filter_stats(stats, type='err_hamiltonian')
    result = defaultdict(list)
    for k, v in extract_stats.items():
        result[k.iter].append((k.time, v))
    for k, _ in result.items():
        result[k] = sorted(result[k], key=lambda x: x[0])

    plt_helper.newfig(textwidth=238.96, scale=0.89)

    # Rearrange data for easy plotting
    err_ham = 1
    for k, v in result.items():
        time = [item[0] for item in v]
        ham = [item[1] for item in v]
        err_ham = ham[-1]
        plt_helper.plt.semilogy(time, ham, '-', lw=1, label='Iter ' + str(k))
    print(err_ham)
    # assert err_ham < 6E-10, 'Error in the Hamiltonian is too large, got %s' % err_ham

    plt_helper.plt.xlabel('Time')
    plt_helper.plt.ylabel('Error in Hamiltonian')
    plt_helper.plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

    fname = 'data/fput_hamiltonian'
    plt_helper.savefig(fname)

    assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
    # assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
    assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'

    # ENERGY PLOTTING #
    # extract error in hamiltonian and prepare for plotting
    result = get_sorted(stats, type='energy_step', sortby='time')

    plt_helper.newfig(textwidth=238.96, scale=0.89)

    # Rearrange data for easy plotting
    for mode in result[0][1].keys():
        time = [item[0] for item in result]
        energy = [item[1][mode] for item in result]
        plt_helper.plt.plot(time, energy, label=str(mode) + 'th mode')

    plt_helper.plt.xlabel('Time')
    plt_helper.plt.ylabel('Energy')
    plt_helper.plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

    fname = 'data/fput_energy'
    plt_helper.savefig(fname)

    assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
    # assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
    assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'

    # POSITION PLOTTING #
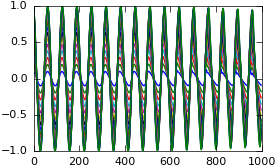
    # extract positions and prepare for plotting
    result = get_sorted(stats, type='position', sortby='time')

    plt_helper.newfig(textwidth=238.96, scale=0.89)

    # Rearrange data for easy plotting
    nparts = len(result[0][1])
    nsteps = len(result)
    pos = np.zeros((nparts, nsteps))
    time = np.zeros(nsteps)
    for idx, item in enumerate(result):
        time[idx] = item[0]
        for n in range(nparts):
            pos[n, idx] = item[1][n]

    for n in range(min(nparts, 16)):
        plt_helper.plt.plot(time, pos[n, :])

    fname = 'data/fput_positions'
    plt_helper.savefig(fname)

    assert os.path.isfile(fname + '.pdf'), 'ERROR: plotting did not create PDF file'
    # assert os.path.isfile(fname + '.pgf'), 'ERROR: plotting did not create PGF file'
    assert os.path.isfile(fname + '.png'), 'ERROR: plotting did not create PNG file'


def main():
    run_simulation()
    show_results()


if __name__ == "__main__":
    main()

Results:

Running fput problem with 1 processors...
   Mean number of iterations: 5.83
   Range of values for number of iterations:  7 
   Position of max/min number of iterations: 475 --  0
   Std and var for number of iterations: 2.10 -- 4.42
... took 37.4485 seconds to run this.

Second-order Problems¶

Simple problems¶

Solar system problem¶

Fermi-Pasta-Ulam-Tsingou problem¶

Table of Contents

Previous topic

Next topic

This Page